题目内容
10.已知长方形的对角线长为1,求长方体的最大的表面积,并求出这时长方体的各棱长.分析 设长方体的各棱长分别为a,b,c,表面积为S,由长方形的对角线长为1,得到a2+b2+c2=1,从而S=2(ab+bc+cd)≤2(a2+b2+c2)=2,由此能求出结果.
解答 解:设长方体的各棱长分别为a,b,c,表面积为S,
∵长方形的对角线长为1,
∴$\sqrt{{a}^{2}+{b}^{2}+{c}^{2}}$=1,∴a2+b2+c2=1,
则有S=2(ab+bc+cd)≤2(a2+b2+c2)=2,
当且仅当a=b=c时,取等号,
这时a=b=c=$\frac{\sqrt{3}}{3}$,
∴长方体的最大的表面积为2,
这时长方体的各条棱长均为$\frac{\sqrt{3}}{3}$.
点评 本题考查长方体的最大表面积及其对应的各棱长的求法,是基础题,解题时要认真审题,注意长方体的性质的合理运用.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
20.设向量$\overrightarrow{a}$=(m,1),$\overrightarrow{b}$=(2,-3),若满足$\overrightarrow{a}⊥\overrightarrow{b}$,则m=( )
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
1.定义在R上的函数f(x)满足:f(x)>1-f′(x),f(0)=4,则不等式$\frac{{{e^x}f(x)}}{{{e^x}+3}}$>1(其中e为自然对数的底数)的解集为( )
| A. | (3,+∞) | B. | (-∞,0)∪(3,+∞) | C. | (0,+∞) | D. | (-∞,0)∪(0,+∞) |
18.4位同学各自在周五、周六、周日三天中任选一天参加公益活动,则三天都有同学参加公益活动的概率为( )
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{26}{27}$ |
5.函数f(x)=sinxcosx-$\frac{\sqrt{3}}{2}$cos2x,则f($\frac{π}{24}$)=( )
| A. | -$\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{6}-\sqrt{2}}{4}$ | D. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ |
20.若双曲线C的顶点和焦点分别为椭圆$\frac{x^2}{9}$+$\frac{y^2}{5}$=1的焦点和顶点,则双曲线C的方程为( )
| A. | $\frac{x^2}{5}-\frac{y^2}{9}=1$ | B. | $\frac{x^2}{9}-\frac{y^2}{5}=1$ | C. | $\frac{x^2}{5}-\frac{y^2}{4}=1$ | D. | $\frac{x^2}{4}-\frac{y^2}{5}=1$ |
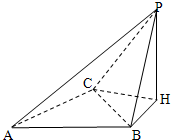 如图,在四面体P-ABC,底面ABC是边长为1的正三角形,AB⊥BP,点P在底面ABC上的射影为H,BH=$\frac{\sqrt{3}}{3}$,平面ACP与平面PBH所成的锐二面角的余弦值为$\frac{\sqrt{6}}{3}$.
如图,在四面体P-ABC,底面ABC是边长为1的正三角形,AB⊥BP,点P在底面ABC上的射影为H,BH=$\frac{\sqrt{3}}{3}$,平面ACP与平面PBH所成的锐二面角的余弦值为$\frac{\sqrt{6}}{3}$.