题目内容

2．若函数f（x）=2xf′（1）+lnx，则f′（1）=-1．

分析 求出函数的导数，然后赋值求解即可．

解答 解：函数f（x）=2xf′（1）+lnx，
可得f′（x）=2f′（1）+$\frac{1}{x}$，
∴f′（1）=2f′（1）+1，
f′（1）=-1．
故答案为：-1．

点评 本题考查对数的应用，考查计算能力．

练习册系列答案
相关题目
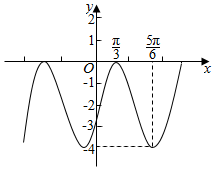12．已知函数f（x）=sinωx（sinωx+2$\sqrt{3}$cosωx）+sin（ωx-$\frac{π}{4}$）sin（ωx+$\frac{π}{4}$）（其中ω为常数，且ω＞0），函数g（x）=f（x）-$\frac{5}{2}$的部分图象如图所示．
（I）求函数g（x）的单凋递减区间；
（Ⅱ）当x∈[-$\frac{π}{6}$，$\frac{π}{4}$]时，求函数f（x）的取值范围．
13．直线y=x+m与椭圆$\frac{{x}^{2}}{16}$$+\frac{{y}^{2}}{9}$=1相交，求m的取值范围．
10．已知cosα=-$\frac{3}{5}$，且sinα＞0，求2cos2（$\frac{π}{8}$-$\frac{α}{2}$）-1的值．
17．若角α的终边上有一点P（-4b，3b）（b≠0），则sinα+cosα=$±\frac{1}{5}$．
7．已知两点P（4，0），Q（0，2），则以线段PQ为直径的圆的方程是（　　）
A．（x+2）2+（y+1）2=5B．（x-2）2+（y-1）2=10C．（x-2）2+（y-1）2=5D．（x+2）2+（y+1）2=10
14．若关于x的方程cos2x-sinx+a=0有解，则a的取值范围是[$-\frac{5}{4}$，1]．
3．已知函数y=f（x）定义在实数集R上的奇函数，且当x∈（-∞，0）时xf′（x）＜-f（x）成立（其中f′（x）是f（x）的导函数），若a=$\sqrt{3}$f（$\sqrt{3}$），b=f（1），c=-2f（log2$\frac{1}{4}$），则a，b，c的大小关系是（　　）
A．c＞a＞bB．c＞b＞aC．a＞b＞cD．a＞c＞b
4．已知对任意的x∈（-∞，0）∪（0，+∞），y∈[-1，1]，不等式x2+$\frac{16}{{x}^{2}}$-2xy-$\frac{8}{x}$$\sqrt{1-{y}^{2}}$-a≥0恒成立，则实数a的取值范围为$（-∞，8-4\sqrt{2}]$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网