题目内容
16.设集合A={x|-1<x<2},B={x|2a-1<x<2a+3}.(1)若A⊆B,求a的取值范围;
(2)若A∩B=∅,求a的取值范围.
分析 (1)根据A⊆B,建立条件关系即可求实数a的取值范围.
(2)根据A∩B=∅,建立条件关系即可求实数a的取值范围.
解答 解:(1)集合A={x|-1<x<2},B={x|2a-1<x<2a+3}.
∵A⊆B,
∴$\left\{{\begin{array}{l}{2a-1≤-1}\\{2a+3≥2}\end{array}}\right.$,
解得:$-\frac{1}{2}≤a≤0$.
故得实数a的取值范围是[$-\frac{1}{2}$,0]
(2)∵A∩B=φ,
∴2a-1≥2或2a+3≤-1,
解得:$a≥\frac{3}{2}$或a≤-2.
故得实数a的取值范围是(-∞,-2]∪[$\frac{3}{2}$,+∞).
点评 本题主要考查集合的基本运算,比较基础.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
6.若$\frac{1+2i}{a+bi}=1+i$,其中a、b为实数,则a+b的值等于( )
| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
7.已知函数f(x)=-3lnx+ax2+bx(a>0,b∈R),若对任意x>0都有f(x)≥f(3)成立,则( )
| A. | lna>-b-1 | B. | lna≥-b-1 | C. | lna≤-b-1 | D. | lna<-b-1 |
4.若函数f( x)=ax3-bx+c为奇函数,则c=( )
| A. | 0 | B. | 1 | C. | -1 | D. | -2 |
3.若函数f(x)=x-2sinxcosx+acosx在[$\frac{π}{4}$,$\frac{3π}{4}$]单调递增,则a的取值范围是( )
| A. | [-3,+∞) | B. | (-∞,-3] | C. | [$\sqrt{2}$,+∞) | D. | (-∞,$\sqrt{2}$] |
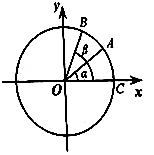 如图,在平面直角坐标系中,以原点为圆心,单位长度为半径的圆上有两点A($\frac{4}{5}$,$\frac{3}{5}$),B($\frac{5}{13}$,$\frac{12}{13}$).
如图,在平面直角坐标系中,以原点为圆心,单位长度为半径的圆上有两点A($\frac{4}{5}$,$\frac{3}{5}$),B($\frac{5}{13}$,$\frac{12}{13}$).