题目内容
若函数f（x）=mx3+x2为偶函数，则实数m的值为 ．
分析：根据函数奇偶性的定义建立方程即可求解m．
解答：解：∵函数f（x）=mx3+x2为偶函数，
∴f（-x）=f（x），
即f（-x）=-mx3+x2=mx3+x2，
∴-m=m，
解得m=0，
故答案为：0．
∴f（-x）=f（x），
即f（-x）=-mx3+x2=mx3+x2，
∴-m=m，
解得m=0，
故答案为：0．
点评：本题主要考查函数奇偶性的应用，利用函数是偶函数，建立方程f（-x）=f（x）是解决本题的关键．
练习册系列答案
备战中考寒假系列答案
相关题目
和圆x2+y2=n2相切，其中m，n∈N，0＜|m-n|≤1，若函数f（x）=mx+1-n的零点x∈（k，k+1）k∈Z，则k= ．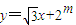
和圆x2+y2=n2相切，其中m，n∈N，0＜|m-n|≤1，若函数f（x）=mx+1-n的零点x∈（k，k+1）k∈Z，则k= ．