题目内容
8.已知正四棱柱ABCD-A1B1C1D1中,AB=1,CC1=2,点E为CC1的中点,则异面直线AC1与BE所成的角等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
分析 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出异面直线AC1与BE所成的角.
解答 解: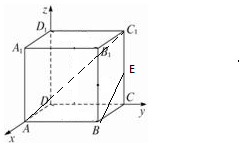 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
则A(1,0,0),C1(0,1,2),B(1,1,0),
E(0,1,1),
$\overrightarrow{A{C}_{1}}$=(-1,1,2),$\overrightarrow{BE}$=(-1,0,1),
设AC1与BE所成角为θ,
则cosθ=$\frac{|\overrightarrow{A{C}_{1}}•\overrightarrow{BE}|}{|\overrightarrow{A{C}_{1}}|•|\overrightarrow{BE}|}$=$\frac{3}{\sqrt{6}•\sqrt{2}}$=$\frac{\sqrt{3}}{2}$,
∴θ=30°.
∴异面直线AC1与BE所成的角为30°.
故选:A.
点评 本题考查异面直线所成角的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是基础题.

练习册系列答案
相关题目
16.函数f(x)=log2x•log22x取得最小值时x的值为( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
3.cos50°($\sqrt{3}$-tan10°)的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | 2 |
17.四个人围坐在一张圆桌旁,每个人面前放着完全相同的硬币,所有人同时翻转自己的硬币.若硬币正面朝上,则这个人站起来; 若硬币正面朝下,则这个人继续坐着.那么,没有相邻的两个人站起来的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{5}{16}$ | C. | $\frac{7}{16}$ | D. | $\frac{11}{16}$ |
18.已知△ABC的三边长分别为a=3,b=4,c=$\sqrt{37}$,则△ABC的面积为( )
| A. | 2$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 6$\sqrt{3}$ | D. | 12$\sqrt{3}$ |