题目内容

19．已知△ABC的面积为S，且$\overrightarrow{AB}$•$\overrightarrow{AC}$=S，则tan2A的值为（　　）
A．$\frac{1}{2}$B．2C．$\frac{3}{4}$D．-$\frac{4}{3}$

分析 由已知和三角形的面积公式可得cosA=$\frac{1}{2}$sinA，进而可得tanA=2，由二倍角的正切公式可得答案

解答 解：设△ABC的角A，B，C所对应的边分别为a，b，c．
∵$\overrightarrow{AB}$•$\overrightarrow{AC}$=S，
∴bccosA=$\frac{1}{2}$bcsinA，
∴tanA=2，
∴tan2A=$\frac{2tanA}{1-ta{n}^{2}A}$=$\frac{2×2}{1-{2}^{2}}$=-$\frac{4}{3}$，
故选：D

点评 本题考查倍角公式、平面向量的运算，属于基础题

练习册系列答案
相关题目
9．如图所示，阴影部分的面积为（　　）
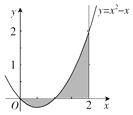
A．$\frac{1}{2}$B．$\frac{2}{3}$C．1D．$\frac{7}{6}$
10．已知函数f（x）=$\left\{\begin{array}{l}{|{x}^{2}-1|，}&{x＜1}\\{\frac{lnx}{x}，}&{x≥1}\end{array}\right.$若方程f（x）=m恰有五个不相等的实数根，则实数m的取值范围为（0，$\frac{1}{e}$）．
7．设函数f（x）=sin2（x+π）-cos2（x-$\frac{π}{3}$）
（1）求f（x）的最小正周期及单调递增区间；
（2）若|f（x）-m|≤2在x∈[-$\frac{π}{6}$，$\frac{π}{4}$]上恒成立，求实数m的取值范围．
14．直线m：kx+y+4=0（k∈R） 是圆C：x2+y2+4x-4y+6=0的一条对称轴，过点A（0，k）作斜率为1的直线n，则直线n被圆C所截得的弦长为（　　）
A．$\sqrt{14}$B．$\sqrt{2}$C．$\sqrt{6}$D．2$\sqrt{6}$
4．已知实数x、y满足$\left\{\begin{array}{l}{2x-y+1≥0}\\{x≥1}\\{x-2y+3≤0}\end{array}\right.$，则$\frac{y}{x}$的取值范围为（$\frac{1}{2}$，3]．
11．若（3-2x）5=a0+a1x+a2x2+…+a5x5，则a0+a1+2a2+3a3+4a4+5a5=233．
8．已知直线ax-y=0（a∈R）与圆C：x2+y2-2ax-2y+2=0交于A，B两点，C为圆心，若∠ACB=$\frac{π}{3}$，则圆C的面积为（　　）
A．8πB．6πC．4πD．2π
9．下列说法正确的是（　　）
A．命题“?x0∈R，2${\;}^{{x}_{0}}$＞1”的否定是“?x∈R，2x≤1”
B．命题“若x=y，则x2=y2”的否命题是“若x=y，则x2≠y2”
C．p：?x∈R，x2+1≥1，q：在△ABC中，若sinA=$\frac{1}{2}$，则A=$\frac{π}{6}$，则p∧q为真命题
D．若平面α⊥平面β，直线a?α，直线b?β，则a⊥b

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网