题目内容
3．某中学田径共有42名队员，其中男生28名、女生14名，采用分层抽样的方法选出6人参加一个座谈会．求运动员甲被抽到的概率以及选出的男、女运动员的人数为$\frac{1}{7}$，4，2．分析 由等可能事件概率计算公式能求出运动员甲被抽到的概率，由分层抽样性质能求出选出的男、女运动员的人数．
解答 解：某中学田径共有42名队员，其中男生28名、女生14名，
采用分层抽样的方法选出6人参加一个座谈会．
运动员甲被抽到的概率p=$\frac{6}{42}$=$\frac{1}{7}$．
男生选出：6×$\frac{28}{28+14}$=4人，
女生选出：6×$\frac{14}{28+14}$=2人．
故答案为：$\frac{1}{7}$，4，2．
点评 本题考查概率的求法，是基础题，解题时要认真审题，注意等可能事件概率计算公式的合理运用．
练习册系列答案
相关题目
13．设全集A={1，2，3，4，5}，B={2，4，6，8，10}，则A∪B=（ ）
| A． | {2，4} | B． | {1，2，3，4，5，6，8，10} | ||
| C． | {1，2，3，4，5} | D． | {2，4，6，8，10} |
11．
一个四棱锥的三视图如图所示，则这个四棱锥的体积等于（ ）
一个四棱锥的三视图如图所示，则这个四棱锥的体积等于（ ）| A． | 8 | B． | 4 | C． | $\frac{8}{3}$ | D． | $\frac{4}{3}$ |
18．设某地若干户家庭的年收入x（单位：万元）和年饮食支出y（单位：万元），调查显示x与y具有线性相关关系，并由调查数据得到y对x的回归直线方程为：$\widehat{y}$=0.254x+0.321．由回归直线方程可知，家庭年收入每增加1万元，则年饮食支出平均增加（ ）
| A． | 0.254万元 | B． | 0.321万元 | C． | 0.575万元 | D． | -0.254万元 |
8．i是虚数单位，复数$\frac{5i}{1-2i}$等于（ ）
| A． | 2-i | B． | 1-2i | C． | -2+i | D． | -1+2i |
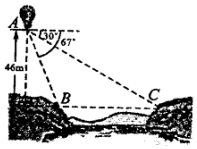如图，从气球A上测得正前方的河流的两岸B，C的俯角分别为67°，30°，此时气球的高是46m，则河流的宽度BC约等于60m．（用四舍五入法将结果精确到个位．参考数据：sin67°≈0.92，cos67°≈0.39，sin37°≈0.60，cos37°≈0.80，$\sqrt{3}$≈1.73．