题目内容
在圆(x-2)2+(y-2)2=4内任取一点,则该点恰好在区域
内的概率为
.
|
| 1 |
| 2π |
| 1 |
| 2π |
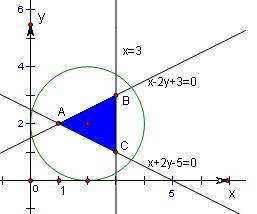
作出不等式组
|
得到如图的△ABC及其内部,其中A(1,2),B(3,3),C(3,1)
∵△ABC位于圆(x-2)2+(y-2)2=4内的部分,
∴在圆(x-2)2+(y-2)2=4内任取一点,则该点恰好在区域
|
| S△ABC |
| S圆 |
| ||
| 22×π |
| 1 |
| 2π |
故答案为:
| 1 |
| 2π |

练习册系列答案
相关题目
已知点B(
,0),点O为坐标原点,点A在圆(x-
)2+(y-
)2=1上,则向量
与
的夹角θ的最大值与最小值分别为( )
| 2 |
| 2 |
| 2 |
| OA |
| OB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 已知点A(x1,y1)在圆(x-2)2+y2=4上运动,点A不与(0,0)重合,点B(4,y0)在直线x=4上运动,动点M(x,y)满足
已知点A(x1,y1)在圆(x-2)2+y2=4上运动,点A不与(0,0)重合,点B(4,y0)在直线x=4上运动,动点M(x,y)满足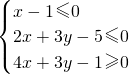 ,点Q(x,y)在圆(x+2)2+(y+2)2=1上,则|PQ|的最大值与最小值为
,点Q(x,y)在圆(x+2)2+(y+2)2=1上,则|PQ|的最大值与最小值为