题目内容
在圆（x-2）2+（y+3）2=2上与点（0，-5）距离最大的点的坐标是（ ）
分析：确定点（0，-5）在圆外，可得圆上与点（0，-5）距离最远的点，在圆心与点（0，-5）连线上，且与点（0，-5）分别在圆心两侧，由此可得结论．
解答：解：∵（0-2）2+（-5+3）2=8＞2
∴点（0，-5）在圆外
∴圆上与点（0，-5）距离最远的点，在圆心与点（0，-5）连线上，且与点（0，-5）分别在圆心两侧令直线解析式：y=kx+b，由于直线通过点（2，-3）和（0，-5）
可得直线解析式：y=x-5，
与圆的方程联立，可得（x-2）2+（x-2）2=2，∴x=3或x=1
∴交点坐标为（3，-2）和（1，-4），其中距离点（0，-5）较大的一个点为（3，-2）
故选D．
∴点（0，-5）在圆外
∴圆上与点（0，-5）距离最远的点，在圆心与点（0，-5）连线上，且与点（0，-5）分别在圆心两侧令直线解析式：y=kx+b，由于直线通过点（2，-3）和（0，-5）
可得直线解析式：y=x-5，
与圆的方程联立，可得（x-2）2+（x-2）2=2，∴x=3或x=1
∴交点坐标为（3，-2）和（1，-4），其中距离点（0，-5）较大的一个点为（3，-2）
故选D．
点评：本题考查点与圆的位置关系，考查直线方程的求解，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
已知点B（
，0），点O为坐标原点，点A在圆（x-
）2+（y-
）2=1上，则向量
与
的夹角θ的最大值与最小值分别为（ ）
| 2 |
| 2 |
| 2 |
| OA |
| OB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知点A（x1，y1）在圆（x-2）2+y2=4上运动，点A不与（0，0）重合，点B（4，y0）在直线x=4上运动，动点M（x，y）满足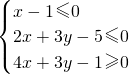
，点Q（x，y）在圆（x+2）2+（y+2）2=1上，则|PQ|的最大值与最小值为