Question

已知点P（x，y）满足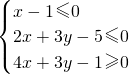，点Q（x，y）在圆（x+2）²+（y+2）²=1上，则|PQ|的最大值与最小值为

1. A.
   6，3
2. B.
   6，2
3. C.
   5，3
4. D.
   5，2

Answer 1

B
分析：先根据条件画出可行域，z=|PQ|，再利用几何意义求最值，只需求出可行域内的点到圆心M（-2，-2）距离的最值，从而得到z最值即可．
解答：先根据约束条件画出可行域，
问题转化为区域内的点到圆心M（-2，-2）的最小值．
∵可行域内点P到圆心M（-2，-2）距离，
当点M到直线4x+3y-1=0的距离时，
z最小，最小值为=3，
∴z=|PQ|的最小值=3-1=2，
由得A（-2，3）
当点M到可行域内的点A（-2，3）距离时，
|MA|最大，最大值为|MA|=5，
∴z=|PQ|的最大值=5+1=6，
故选B．
点评：本题主要考查了简单的线性规划，以及利用几何意义求最值，属于基础题．