题目内容
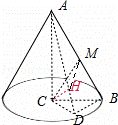
等腰Rt△ACB,AB=2, .以直线AC为轴旋转一周得到一个圆锥,D为圆锥底面一点,BD⊥CD,CH⊥AD于点H,M为AB中点,则当三棱锥C﹣HAM的体积最大时,CD的长为( )
.以直线AC为轴旋转一周得到一个圆锥,D为圆锥底面一点,BD⊥CD,CH⊥AD于点H,M为AB中点,则当三棱锥C﹣HAM的体积最大时,CD的长为( )
|
| A. |
| B. |
| C. |
| D. |
|
C.
【解析】根据题意,得
∵AC⊥平面BCD,BD⊂平面BCD,∴AC⊥BD,
∵CD⊥BD,AC∩CD=C,∴BD⊥平面ACD,可得BD⊥CH,
∵CH⊥AD,AD∩BD=D,∴CH⊥平面ABD,可得CH⊥AB,
∵CM⊥AB,CH∩CM=C,∴AB⊥平面CMH,
因此,三棱锥C﹣HAM的体积V=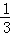 S△CMH×AM=
S△CMH×AM=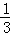 S△CMH由此可得,当S△CMH达到最大值时,三棱锥C﹣HAM的体积最大
S△CMH由此可得,当S△CMH达到最大值时,三棱锥C﹣HAM的体积最大
设∠BCD=θ,则Rt△BCD中,BC=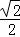 AB=
AB=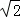
可得CD=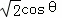 ,BD=
,BD=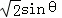
Rt△ACD中,根据等积转换得CH=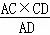 =
=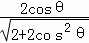
Rt△ABD∽Rt△AHM,得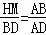 ,所以HM=
,所以HM=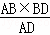 =
=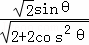
因此,S△CMH=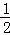 CH•HM=
CH•HM=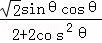 =
=
∵4+2tan2θ≥4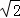 tanθ,
tanθ,
∴S△CMH= ≤
≤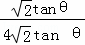 =
=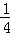 ,
,
当且仅当tanθ=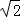 时,S△CMH达到最大值,三棱锥C﹣HAM的体积同时达到最大值.
时,S△CMH达到最大值,三棱锥C﹣HAM的体积同时达到最大值.
∵tanθ=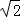 >0,可得sinθ=
>0,可得sinθ=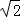 cosθ>0
cosθ>0
∴结合sin2θ+cos2θ=1,解出cos2θ=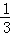 ,可得cosθ=
,可得cosθ=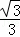 (舍负)
(舍负)
由此可得CD=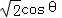 =
=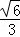 ,
,
即当三棱锥C﹣HAM的体积最大时,CD的长为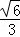
故选:C

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目




 与
与 轴相交于An,Bn两点,则
轴相交于An,Bn两点,则 (3,1),若
(3,1),若 ,,则P(2<X<4)=
,,则P(2<X<4)= ( B)l—p (C)l-2p (D)
( B)l—p (C)l-2p (D)

 围成的区域内(阴影部分)的概率为( )
围成的区域内(阴影部分)的概率为( )
 B.
B.  C.
C.  D.
D. 
 =m
=m ,
, =n
=n (m•n≠0),若
(m•n≠0),若 ∥
∥ ,则
,则 =___________________.
=___________________.
 ,则圆锥的体积为 .
,则圆锥的体积为 . ,三个内角
,三个内角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 ,若内角
,若内角 的解集为
的解集为 ,则
,则 B.
B. C.
C. D.
D.