题目内容
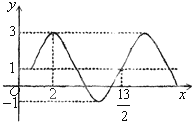 函数y=Asin(ωx+φ)+k(A>0,φ>0,|φ|<
函数y=Asin(ωx+φ)+k(A>0,φ>0,|φ|<| π | 2 |
分析:由图可求k,A,由又
T=
-2=
,可求得ω,利用2ω+φ=2kπ+
(k∈Z)与|φ|<
可求φ,从而可得函数表达式,利用正弦函数的性质可求函数的最小正周期,单调区间.
| 3 |
| 4 |
| 13 |
| 2 |
| 9 |
| 2 |
| π |
| 2 |
| π |
| 2 |
解答:解:∵k=
=1,
∴A=2;
又
T=
-2=
,
∴T=
=6(ω>0),
∴ω=
;
又2ω+φ=2kπ+
,k∈Z
∴φ=2kπ-
(k∈Z),又|φ|<
,
∴φ=-
.
∴函数解析式为y=2sin(
x-
)+1;
由2kπ-
≤
x-
≤2kπ+
得:6k-1≤x≤6k+2(k∈Z);
∴该函数的单调增区间为[6k-1,6k+2](k∈z);
同理,由2kπ+
≤
x-
≤2kπ+
得该函数的单调减区间为[6k+2,6k+5](k∈z).(12分)
| 3+(-1) |
| 2 |
∴A=2;
又
| 3 |
| 4 |
| 13 |
| 2 |
| 9 |
| 2 |
∴T=
| 2π |
| ω |
∴ω=
| π |
| 3 |
又2ω+φ=2kπ+
| π |
| 2 |
∴φ=2kπ-
| π |
| 6 |
| π |
| 2 |
∴φ=-
| π |
| 6 |
∴函数解析式为y=2sin(
| π |
| 3 |
| π |
| 6 |
由2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
∴该函数的单调增区间为[6k-1,6k+2](k∈z);
同理,由2kπ+
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
| 3π |
| 2 |
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查正弦函数的单调性,考查运算能力,属于中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
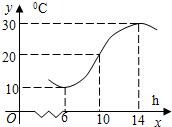 如图所示,某地一天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b,则8时的温度大约为
如图所示,某地一天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b,则8时的温度大约为
 如图,是函数y=Asin(ωx+φ),(-π<φ<π)的图象的一段,O是坐标原点,P是图象的最高点,A点坐标为(5,0),若
如图,是函数y=Asin(ωx+φ),(-π<φ<π)的图象的一段,O是坐标原点,P是图象的最高点,A点坐标为(5,0),若