题目内容
若函数y=Asin(ωx+φ)(ω>0)与x轴的两个相邻的交点坐标为(-4,0),(2,0),则ω=分析:欲求ω,先求函数的周期,题目中给出的两个交点的横坐标之差的绝对值即为半个周期,从而可求得ω
解答:解:∵函数y=Asin(ωx+φ)(ω>0)与x轴的两个相邻的交点坐标为(-4,0),(2,0)
∴
T=2-(-4)=6,∴T=12
又∵T=2π/ω,∴ω=
=
.
故答案为:
∴
| 1 |
| 2 |
又∵T=2π/ω,∴ω=
| 2π |
| 12 |
| π |
| 6 |
故答案为:
| π |
| 6 |
点评:本题主要考查有函数y=Asin(ωx+φ)的图象确定函数解析式,关键是周期公式T=2π/ω的应用.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
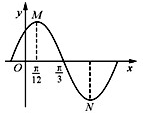 若函数y=Asin(ωx+φ),(A>0,ω>0,|φ|<
若函数y=Asin(ωx+φ),(A>0,ω>0,|φ|<| π |
| 2 |
| OM |
| ON |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若函数y=Asin(ωx+φ)+m的最大值为4,最小值为0,最小正周期为
,直线x=
是其图象的一条对称轴,则它的解析式是( )
| π |
| 2 |
| π |
| 3 |
A、y=4sin(4x+
| ||
B、y=2sin(2x+
| ||
C、y=2sin(4x+
| ||
D、y=2sin(4x+
|
 (2012•吉林二模)若函数y=Asin(ωx+φ)+b(A>0,ω>0,|φ|<
(2012•吉林二模)若函数y=Asin(ωx+φ)+b(A>0,ω>0,|φ|< (2012•蚌埠模拟)若函数
(2012•蚌埠模拟)若函数