题目内容
【题目】已知函数![]() ,
,![]() 在一个周期内的图像如图所示.
在一个周期内的图像如图所示.
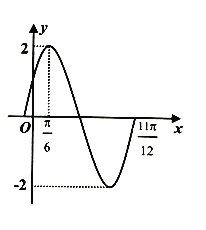
(I)求函数![]() 的解析式;
的解析式;
(II)设![]() ,且方程
,且方程![]() 有两个不同的实数根,求实数
有两个不同的实数根,求实数![]() 的取值范围以及这两个根的和.
的取值范围以及这两个根的和.
【答案】(Ⅰ)![]() .(Ⅱ)见解析.
.(Ⅱ)见解析.
【解析】
(I)根据三角函数的图像的最高点,求得![]() 的值,根据三角函数的周期,求得
的值,根据三角函数的周期,求得![]() 的值,根据函数图像上的特殊点,求得
的值,根据函数图像上的特殊点,求得![]() 的值,由此求得函数的解析式.(II)画出函数
的值,由此求得函数的解析式.(II)画出函数![]() 的图像与函数
的图像与函数![]() 的图像,根据图像求得
的图像,根据图像求得![]() 的的取值范围.根据对称性求得两根的和.
的的取值范围.根据对称性求得两根的和.
(I)由题设图象,易得![]() ,
,![]() ,
,
所以![]() ,所以
,所以![]() .
.
所以![]() .
.
因为函数![]() 的图象经过点
的图象经过点![]() ,
,
所以![]() ,即
,即![]() .
.
又因为![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() .
.
故所求函数![]() 的解析式为
的解析式为![]() .
.
(Ⅱ)由题意,知方程![]() 有两个不同的实数根等价于函数
有两个不同的实数根等价于函数![]() 的图象与
的图象与![]() 的图象有两个不同的交点.
的图象有两个不同的交点.
因为![]() ,
,
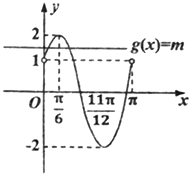
易画出函数![]() 的图象与函数
的图象与函数![]() 的图象(如图所示).
的图象(如图所示).
依据图象可知:
当![]() 或
或![]() 时,
时,
直线![]() 与曲线
与曲线![]() 有两个不同的交点,
有两个不同的交点,
即方程![]() 有两个不同的实数根,
有两个不同的实数根,
故所求实数![]() 的取值范围为
的取值范围为![]() .
.
①当![]() 时,
时,![]() 与
与![]() 的图象有两交点且关于直线
的图象有两交点且关于直线![]() 对称,设此时方程
对称,设此时方程![]() 两个不同的实数根分别为
两个不同的实数根分别为![]() ,
,![]() ,
,
所以当![]() ,即
,即![]()
②当![]() 时,
时,![]() 与
与![]() 的图象有两交点且关于直线
的图象有两交点且关于直线![]() 对称,设此时方程
对称,设此时方程![]() 两个不同的实数根分别为
两个不同的实数根分别为![]() ,
,![]() ,
,
所以![]() ,即
,即![]()
综上,当![]() 时,所求方程的两根之和为
时,所求方程的两根之和为![]()
当![]() 时,所求方程的两根之和为
时,所求方程的两根之和为![]() .
.

练习册系列答案
相关题目
【题目】随着手机的普及,大学生迷恋手机的现象非常严重.为了调查双休日大学生使用手机的时间,某机构采用不记名方式随机调查了使用手机时间不超过![]() 小时的
小时的![]() 名大学生,将
名大学生,将![]() 人使用手机的时间分成
人使用手机的时间分成![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别加以统计,得到下表,根据数据完成下列问题:
分别加以统计,得到下表,根据数据完成下列问题:
使用时间/时 |
|
|
|
|
|
大学生/人 |
|
|
|
|
|

(1)完成频率分布直方图;
(2)根据频率分布直方图估计大学生使用手机的平均时间.
