题目内容
【题目】已知椭圆C： 
(a>b>0)的一个顶点为A(2,0)，离心率为
.直线y＝k(x－1)与椭圆C交于不同的两点M，N.
(1)求椭圆C的方程；
(2)当△AMN的面积为
时，求k的值．
【答案】（1）
（2）1或－1.
【解析】试题分析：（I）由已知条件可得
和
的值，利用
可得
的值，进而可得椭圆的方程；（II）先设
、
的坐标，再联立直线
的方程和椭圆的方程，消去
，化简得关于
的一元二次方程，由韦达定理可得
，
的值，由弦长公式求|MN|，由点到直线的距离公式求△AMN的高，再根据三角形的面积求
．
试题解析：（1）由题意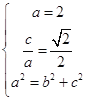得
解得
．所以椭圆C的方程为
．
（2）由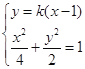
得
．
设点M，N的坐标分别为
，
，则
，
，
，
．
所以|MN|=
=
=
．
由因为点A（2,0）到直线
的距离
，
所以△AMN的面积为
． 由
，解得
，经检验
，所以
．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
