题目内容
17.一个口袋内装有大小相同的6个球,其中3个白球,3个黑球,从中一次摸出两个球,则摸出的两个球至少一个是白球的概率是$\frac{4}{5}$.分析 基本事件总数n=${C}_{6}^{2}$=15,摸出的两个球至少一个是白球的对立事件是摸出的两球都是黑球,由此利用对立事件概率计算公式能求出摸出的两个球至少一个是白球的概率.
解答 解:∵一个口袋内装有大小相同的6个球,其中3个白球,3个黑球,从中一次摸出两个球,
基本事件总数n=${C}_{6}^{2}$=15,
摸出的两个球至少一个是白球的对立事件是摸出的两球都是黑球,
∴摸出的两个球至少一个是白球的概率:
p=1-$\frac{{C}_{3}^{2}}{{C}_{6}^{2}}$=$\frac{4}{5}$.
故答案为:$\frac{4}{5}$.
点评 本题考查概率的求法,考查推理论证能力、运算求解能力,考查化归转化思想、函数与方程思想,是基础题.

练习册系列答案
相关题目
8.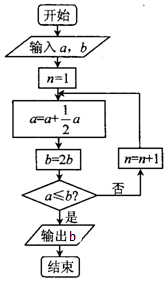 宋元时期数学名著《算学启蒙》中关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等,如图是源于其思想的一个程序框图,若输入的a,b分别为5,2,则输出的b=( )
宋元时期数学名著《算学启蒙》中关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等,如图是源于其思想的一个程序框图,若输入的a,b分别为5,2,则输出的b=( )
 宋元时期数学名著《算学启蒙》中关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等,如图是源于其思想的一个程序框图,若输入的a,b分别为5,2,则输出的b=( )
宋元时期数学名著《算学启蒙》中关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等,如图是源于其思想的一个程序框图,若输入的a,b分别为5,2,则输出的b=( )| A. | 8 | B. | 16 | C. | 32 | D. | 64 |
2.高三某班有50名学生,一次数学考试的成绩ξ服从正态分布:ξ~N(105,102),已知P(95≤ξ≤105)=0.3413,该班学生此次考试数学成绩在115分以上的概率为( )
| A. | 0.1587 | B. | 0.3413 | C. | 0.1826 | D. | 0.5000 |
9.集合$A=\left\{{x\left|{\frac{x+2}{x-2}≤0}\right.}\right\}$,B={x|x-1≥0},则A∩B为( )
| A. | [1,2] | B. | [1,2) | C. | [-2,∞) | D. | (-2,2] |
6.复数$z=\frac{10i}{1+3i}$(其中i为虚数单位),$\overline z$为z的共轭复数,则下列结论正确的是( )
| A. | z=-3+i | B. | $\overline z=3-i$ | C. | z=1-3i | D. | $\overline z=-1+3i$ |
 如图,点A(2,0),直线l垂直y轴,垂足为点B,线段AB的垂直平分线与l相交于点C,
如图,点A(2,0),直线l垂直y轴,垂足为点B,线段AB的垂直平分线与l相交于点C,