题目内容
求曲线y=解: ![]()
![]() =
=![]()
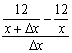
=12![]()
![]()
=12![]()
![]() ,
,
∴y '|x=3=![]() .
.
∴点P处的切线方程为y-4=-![]() (x-3),
(x-3),
即4x+3y-24=0.
点评:求切线方程关键在于利用导数的定义求出斜率.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
求曲线y=解: ![]()
![]() =
=![]()
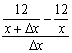
=12![]()
![]()
=12![]()
![]() ,
,
∴y '|x=3=![]() .
.
∴点P处的切线方程为y-4=-![]() (x-3),
(x-3),
即4x+3y-24=0.
点评:求切线方程关键在于利用导数的定义求出斜率.

 阅读快车系列答案
阅读快车系列答案