题目内容
(14分)已知函数f(x)=ex﹣m﹣ln(2x).
(Ⅰ)设x=1是函数f(x)的极值点,求m的值并讨论f(x)的单调性;
(Ⅱ)当m≤2时,证明:f(x)>﹣ln2.
(Ⅰ) ,函数f(x)在(0,1)上单调递减,在(1,+∞)上单调递增.
,函数f(x)在(0,1)上单调递减,在(1,+∞)上单调递增.
(Ⅱ)详见解析:
【解析】
试题分析:
(Ⅰ)首先由函数 的解析式求出其导数
的解析式求出其导数 ,根据题意有
,根据题意有 ,解此方程可得
,解此方程可得 的值,从而确定函数
的值,从而确定函数 的导数
的导数 的表达式,再利用导数的符号判断函数的单调性;
的表达式,再利用导数的符号判断函数的单调性;
(Ⅱ) 时,
时, 恒成立,取函数
恒成立,取函数
于是当 时,可得:
时,可得: ,问题得证.
,问题得证.
试题解析:(Ⅰ)【解析】
∵f(x)=ex﹣m﹣ln(2x),
∴f′(x)=ex﹣m﹣ ,
,
由x=1是函数f(x)的极值点得f′(1)=0,
即e1﹣m﹣1=0,∴m=1. (2分)
于是f(x)=ex﹣1﹣ln(2x),f′(x)=ex﹣1﹣ ,
,
由f″(x)=ex﹣1+ >0知 f′(x)在x∈(0,+∞)上单调递增,且f′(1)=0,
>0知 f′(x)在x∈(0,+∞)上单调递增,且f′(1)=0,
∴x=1是f′(x)=0的唯一零点. (4分)
因此,当x∈(0,1)时,f'(x)<0,f(x)递减;
x∈(1,+∞)时,f'(x)>0,f(x)递增,
∴函数f(x)在(0,1)上单调递减,在(1,+∞)上单调递增. (6分)
(Ⅱ)证明:当m≤2,x∈(0,+∞)时,ex﹣m≥ex﹣2,
又ex≥x+1,∴ex﹣m≥ex﹣2≥x﹣1. (8分)
取函数h(x)=x﹣1﹣ln(2x)(x>0),h′(x)=1﹣ ,
,
当0<x<1时,h′(x)<0,h(x)单调递减;当x>1时,h′(x)>0,h(x)单调递增,得函数h(x)在x=1时取唯一的极小值即最小值为h(1)=﹣ln2. (12分)
∴f(x)=ex﹣m﹣ln(2x)≥ex﹣2﹣ln(2x)≥x﹣1﹣ln(2x)≥﹣ln2,
而上式三个不等号不能同时成立,故f(x)>﹣ln2.(14分)
考点:导数在研究函数性质中的应用综合问题.

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案(本小题满分12分)某普通高中高三年级共有 人,分三组进行体质测试,在三个组中男、女生人数如下表所示.已知在全体学生中随机抽取
人,分三组进行体质测试,在三个组中男、女生人数如下表所示.已知在全体学生中随机抽取 名,抽到第二、三组中女生的概率分别是
名,抽到第二、三组中女生的概率分别是 、
、 .
.
第一组 | 第二组 | 第三组 | |
女生 |
|
|
|
男生 |
|
|
|
(1)求 ,
, ,
, 的值;
的值;
(2)为了调查学生的课外活动时间,现从三个组中按 的比例抽取学生进行问卷调查,三个组被选取的人数分别是多少?
的比例抽取学生进行问卷调查,三个组被选取的人数分别是多少?
(3)若从(2)中选取的学生中随机选出两名学生进行访谈,求参加访谈的两名学生“来自两个组”的概率.






 的虚部是( )
的虚部是( ) B.
B. C.
C. D.
D.
 ),则下列结论正确的是( )
),则下列结论正确的是( ) ,0)对称
,0)对称 ]上为增函数
]上为增函数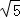 的概率为 _________ .
的概率为 _________ . sin2x+
sin2x+ cos2x,若将函数f(x)的图象向右平移
cos2x,若将函数f(x)的图象向右平移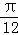 个单位,所得图象对应函数为g(x),则( )
个单位,所得图象对应函数为g(x),则( )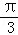 对称,g(x)图象关于原点对称
对称,g(x)图象关于原点对称 ,0)对称,g(x)图象关于直线x=
,0)对称,g(x)图象关于直线x= 对称,g(x)图象关于原点对称
对称,g(x)图象关于原点对称 ,0)对称,g(x)图象关于直线x=
,0)对称,g(x)图象关于直线x= 满足
满足 ,则不等式组所表示的平面区域的面积为_________.
,则不等式组所表示的平面区域的面积为_________. 在
在 不是单调函数,则
不是单调函数,则 的范围是 .
的范围是 .