题目内容
设z=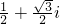 ,那么z+z2+z3+z4+z5+z6=________.
,那么z+z2+z3+z4+z5+z6=________.
0
分析:应用复数三角形式的乘方法则求得 z6=cos2π+isin2π=1,再由 z+z2+z3+z4+z5+z6 = 求出结果.
求出结果.
解答:∵z=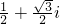 =cos
=cos +isin
+isin ,∴z6=cos2π+isin2π=1,∴z+z2+z3+z4+z5+z6 =
,∴z6=cos2π+isin2π=1,∴z+z2+z3+z4+z5+z6 = =0,
=0,
故答案为:0.
点评:本题主要考查等比数列的前n项和公式,复数三角形式的乘方法则的应用,属于基础题.
分析:应用复数三角形式的乘方法则求得 z6=cos2π+isin2π=1,再由 z+z2+z3+z4+z5+z6 =
 求出结果.
求出结果.解答:∵z=
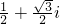 =cos
=cos +isin
+isin ,∴z6=cos2π+isin2π=1,∴z+z2+z3+z4+z5+z6 =
,∴z6=cos2π+isin2π=1,∴z+z2+z3+z4+z5+z6 = =0,
=0,故答案为:0.
点评:本题主要考查等比数列的前n项和公式,复数三角形式的乘方法则的应用,属于基础题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 为实数,且
为实数,且 .
. ,那么z+z2+z3+z4+z5+z6= .
,那么z+z2+z3+z4+z5+z6= .