题目内容
图是函数y=f（x）的导函数y=f′（x）的图象，给出下列命题：
①-3是函数y=f（x）的极值点；
②-1是函数y=f（x）的最小值点；
③y=f（x）在x=0处切线的斜率小于零；
④y=f（x）在区间（-3，1）上单调递增．
则正确命题的序号是（ ）
①-3是函数y=f（x）的极值点；
②-1是函数y=f（x）的最小值点；
③y=f（x）在x=0处切线的斜率小于零；
④y=f（x）在区间（-3，1）上单调递增．
则正确命题的序号是（ ）
| A．①② | B．②③ | C．③④ | D．①④ |
由导函数y=f′（x）的图象知
f（x）在（-∞，-3）单调递减，（-3，+∞）单调递增
所以①-3是函数y=f（x）的极小值点，即最小值点
故①对②不对
∵0∈，（-3，+∞）
又在（-3，+∞）单调递增
∴f′（0）＞0
故③错
∵f（x）在（-3，+∞）单调递增
∴y=f（x）在区间（-3，1）上单调递增
故④对
故选D
f（x）在（-∞，-3）单调递减，（-3，+∞）单调递增
所以①-3是函数y=f（x）的极小值点，即最小值点
故①对②不对
∵0∈，（-3，+∞）
又在（-3，+∞）单调递增
∴f′（0）＞0
故③错
∵f（x）在（-3，+∞）单调递增
∴y=f（x）在区间（-3，1）上单调递增
故④对
故选D
练习册系列答案
相关题目
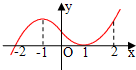如图是函数y=f（x）的导函数y=f′（x）的图象，给出下列命题：
如图是函数y=f（x）的图象，f（f（2））的值为（ ）
如图是函数y=f（x）的导函数y=f′（x）的图象，则下列说法正确的是（ ）
（2012•茂名一模）如图是函数y=f（x）的导函数y=f′（x）的图象，给出下列命题：
（2009•河东区二模）如图是函数y=f（x）的图象的一部分，则f（x）可以是（ ）