题目内容
设函数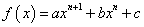
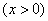 ,其中
,其中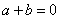 ,
,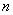 为正整数,
为正整数,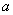 、
、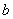 、
、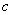 均为常数,曲线
均为常数,曲线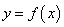 在
在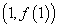 处的切线方程为
处的切线方程为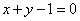 .
.
(1)求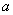 、
、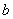 、
、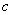 的值;
的值;
(2)求函数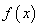 的最大值;
的最大值;
(3)证明:对任意的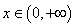 都有
都有 .(
.( 为自然对数的底)
为自然对数的底)

 在区间内成立,再令
在区间内成立,再令 ,得到
,得到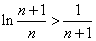 ,最终得到
,最终得到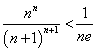 ,再结合(2)中的结论得到
,再结合(2)中的结论得到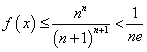 .
.

证法2:令 ,则
,则 .
.
当 时,
时,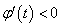 ,故
,故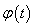 在
在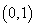 上单调递减;
上单调递减;
而当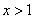 时,
时, 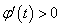 ,故
,故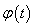 在
在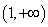 上单调递增.
上单调递增.
 在
在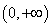 上有最小值,
上有最小值, .
.
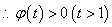 ,即
,即 .
.
令 ,得
,得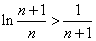 ,即
,即 ,所以
,所以 ,即
,即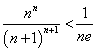 .
.
由(2)知,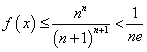 ,故所证不等式成立.
,故所证不等式成立.
考点:1.利用导数求切线方程;2.利用导数求函数的最值;3.函数不等式

练习册系列答案
相关题目
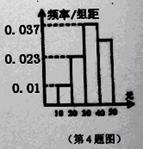
某单位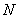 名员工参加“社区低碳你我他”活动.他们的年龄在
名员工参加“社区低碳你我他”活动.他们的年龄在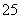 岁至
岁至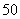 岁之间.按年龄分组:第1组
岁之间.按年龄分组:第1组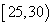 ,第
,第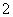 组
组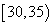 ,第3组
,第3组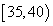 ,第
,第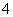 组
组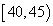 ,第
,第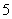 组
组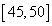 ,得到的频率分布直方图如图5所示.下表是年龄的频率分布表.
,得到的频率分布直方图如图5所示.下表是年龄的频率分布表.
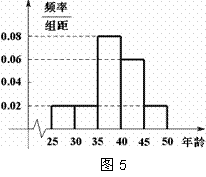

| 区间 |
|
|
|
|
|
| 人数 |
|
|
|
(1)求正整数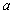 、
、 、
、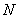 的值;
的值;
(2)现要从年龄较小的第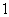 、
、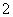 、
、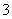 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取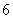 人,则年龄在第
人,则年龄在第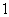 、
、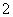 、
、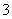 组的人数分别
组的人数分别
是多少?
(3)在(2)的条件下,从这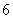 人中随机抽取
人中随机抽取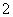 人参加社区宣传交流活动,求恰有
人参加社区宣传交流活动,求恰有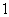 人在第
人在第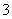 组的概率.
组的概率.
 中,曲线
中,曲线 的焦点
的焦点 ,点
,点 在曲线
在曲线 上,
上, 为圆心的圆与曲线
为圆心的圆与曲线 ,则
,则 .
. ,1)在直线
,1)在直线 的右下方,则
的右下方,则 、
、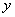 满足约束条件
满足约束条件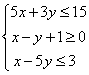 ,则
,则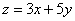 的最小值为( )
的最小值为( )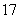 B.
B.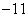 C.
C.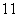 D.
D.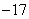
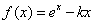 .
.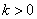 ,且对于任意
,且对于任意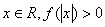 恒成立,试确定实数
恒成立,试确定实数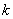 的取值范围;
的取值范围; ,
,
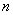 个同学进行调查,结果显示这些同学的支出都在
个同学进行调查,结果显示这些同学的支出都在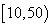 (单位:元),其中支出在
(单位:元),其中支出在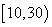 (单位:元)的同学有
(单位:元)的同学有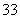 人,其频率分布直方图如下图所示,则支出在
人,其频率分布直方图如下图所示,则支出在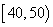 (单位:元)的同学人数是( )
(单位:元)的同学人数是( )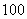 B.
B.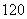 C.
C.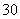 D.
D.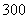
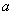
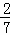 ,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取…,取球后不放回,直到两人中有一人取到白球时终止,每个球在每一次被取出的机会是等可能的,用ξ表示取球终止所需要的取球次数.
,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取…,取球后不放回,直到两人中有一人取到白球时终止,每个球在每一次被取出的机会是等可能的,用ξ表示取球终止所需要的取球次数. 的右焦点,且与直线
的右焦点,且与直线 相切的圆方程是 ________;
相切的圆方程是 ________;