题目内容
9.等差数列-1,2,5,8,…的通项公式是an=3n-4,3n-1是该数列的第n+1项.分析 由等差数列-1,2,5,8,…可得首项与公差,再利用通项公式即可得出.
解答 解:由等差数列-1,2,5,8,…可得首项为-1,公差为2-(-1)=3.
∴通项公式是an=-1+3(n-1)=3n-4,
3n-1是该数列的第n+1项.
故答案分别为:an=3n-4;n+1.
点评 本题考查了等差数列的通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.已知函数g(x)的图象与函数f(x)=|ln(x+a)|-1的图象关于原点对称,且两个图象恰有三个不同的交点,则实数a的值为( )
| A. | $\frac{1}{e}$ | B. | 1 | C. | e | D. | e2 |
19.sin50°cos35°+sin40°sin(-35°)=( )
| A. | $\frac{\sqrt{6}-\sqrt{2}}{4}$ | B. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ | C. | $\frac{\sqrt{2}-\sqrt{6}}{4}$ | D. | $-\frac{\sqrt{6}+\sqrt{2}}{4}$ |
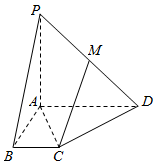 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥BC,BC∥AD,AB=BC=1,AD=2,M为PD的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥BC,BC∥AD,AB=BC=1,AD=2,M为PD的中点.