题目内容
1.已知函数g(x)的图象与函数f(x)=|ln(x+a)|-1的图象关于原点对称,且两个图象恰有三个不同的交点,则实数a的值为( )| A. | $\frac{1}{e}$ | B. | 1 | C. | e | D. | e2 |
分析 根据函数的对称性可得f(x)=-f(-x)有3个不同的零点,由于f(x)=-f(x)由奇数个零点,故f(0)=0,解得a=e或a=$\frac{1}{e}$,分两种情况画图验证零点的个数即可
解答 解:g(x)与f(x)的图象关于原点对称,
∴g(x)=-f(x),
∴f(x)=-f(-x)有3个不同的零点,
∴f(0)=|lna|-1=0,
∴a=e或a=$\frac{1}{e}$,
当a=e时,y=-f(-x)和y=f(x)的图象如下,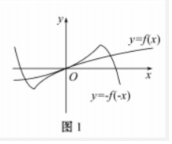
由图象可知,a=e时,符合条件
当a=$\frac{1}{e}$时,y=-f(-x)和y=f(x)的图象如下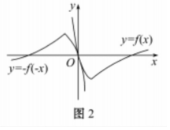
由图象可知,a=$\frac{1}{e}$时,只有1个交点,不符合条件,
综上所述∴a=e,
故选:C.
点评 本题考查了根的存在性及根的个数判断,以及函数与方程的思想,属于中档题.

练习册系列答案
相关题目
13.cos$\frac{π}{7}$cos$\frac{3π}{7}$cos$\frac{5π}{7}$的值为( )
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | $\frac{1}{8}$ | D. | -$\frac{1}{8}$ |
10.已知弹簧拉长0.02m需要98N的力,则把弹簧拉长0.1m所做的功为( )
| A. | 24.5J | B. | 23.5J | C. | 22.5J | D. | 25.0J |
11.某市为了“还城一片蓝天”,决定大力发展公共交通,市物价局举行地铁票价定价听证会,讨论地铁的价格与老百姓的承受能力.消费者代表为440名,市政府、工会、消保委代表是460名,其他是(专家、经营者等)是500名,用分层抽样的方法从中抽取70名代表进行抽样凋查,对地铁的“服务满意度”与“价格满意度”都分为五个等级:1级(很不满意);2级(不满意);3级(一般);4级(满意);5级(很满意),其统计结果如表(服务满意度为x,价格满意度为y).
(1)求市政府、工会、消保委代表抽取的人数;
(2)求“服务满意度”为3时的5个“价格满意度”数据的方差.
 | 价格满意度 | |||||
| 1 | 2 | 3 | 4 | 5 | ||
| 服务满意度 | 1 | 1 | 1 | 2 | 2 | 0 |
| 2 | 2 | 1 | 3 | 4 | 1 | |
| 3 | 3 | 7 | 8 | 8 | 4 | |
| 4 | 1 | 4 | 6 | 4 | 1 | |
| 5 | 0 | 1 | 2 | 3 | 1 | |
(2)求“服务满意度”为3时的5个“价格满意度”数据的方差.
 如图所示,-家电商根据以往某种热销产品的销售记录,绘制了这种商品日销售的频率分布直方图,若-个月以30天计算,估计该家电商一个月内这种商品日销售不少于150个的天数9.
如图所示,-家电商根据以往某种热销产品的销售记录,绘制了这种商品日销售的频率分布直方图,若-个月以30天计算,估计该家电商一个月内这种商品日销售不少于150个的天数9.