题目内容

（1）设log34·log48·log8m=log416，求m；
（2）已知log142=a，用a表示。
解：（1）利用换底公式，得
∴lgm=2lg3，于是m=9；
（2）由对数换底公式，得

。
练习册系列答案
相关题目
设函数f(x)=log3
x+2
x
-a在区间（1，2）内有零点，则实数a的取值范围是（　　）
A、（-1，-log32）
B、（0，log32）
C、（log32，1）
D、（1，log34）
计算：
（1）2log510+log50.25；
（2）设10m=2，10n=3，求103m+n=？
（3）log2(47×25)-lg
4100
+log23•log34．
（2011•温州二模）设函数f(x)=
3x，x≤1
f(
x
2
) ，x＞1
，则f（log34）的值为
2
2
．
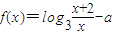设函数在区间（1，2）内有零点，则实数a的取值范围是（ ）
A．（-1，-log32）
B．（0，log32）
C．（log32，1）
D．（1，log34）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网