题目内容
计算:
(1)2log510+log50.25;
(2)设10m=2,10n=3,求103m+n=?
(3)log2(47×25)-lg
+log23•log34.
(1)2log510+log50.25;
(2)设10m=2,10n=3,求103m+n=?
(3)log2(47×25)-lg
| 4 | 100 |
分析:(1)化小数为分数后直接利用对数式的运算性质化简求值;
(2)由已知求出m和n的值,代入103m+n后利用对数式的运算性质化简求值;
(3)化根式为分数指数幂,然后直接利用对数式的运算性质化简求值.
(2)由已知求出m和n的值,代入103m+n后利用对数式的运算性质化简求值;
(3)化根式为分数指数幂,然后直接利用对数式的运算性质化简求值.
解答:解:(1)2log510+log50.25
=2log5(2×5)+2log50.5
=2log52+2+2log5
=2;
(2)由10m=2,10n=3,
则m=lg2,n=lg3.
103m+n=103lg2+lg3=10lg24=24;
(3)log2(47×25)-lg
+log23•log34
=log2214+log225-lg10
+2•
•
=19-
+2=
.
=2log5(2×5)+2log50.5
=2log52+2+2log5
| 1 |
| 2 |
=2;
(2)由10m=2,10n=3,
则m=lg2,n=lg3.
103m+n=103lg2+lg3=10lg24=24;
(3)log2(47×25)-lg
| 4 | 100 |
=log2214+log225-lg10
| 1 |
| 2 |
| lg3 |
| lg2 |
| lg2 |
| lg3 |
=19-
| 1 |
| 2 |
| 41 |
| 2 |
点评:本题考查了对数式的运算性质,考查了有理指数幂的运算性质,是基础的计算题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
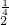
 -1)0+(
-1)0+( )
)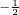 +(
+( )
)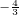 .
.