题目内容
设函数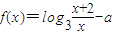 在区间(1,2)内有零点,则实数a的取值范围是( )
在区间(1,2)内有零点,则实数a的取值范围是( )A.(-1,-log32)
B.(0,log32)
C.(log32,1)
D.(1,log34)
【答案】分析:由函数在区间(1,2)内有零点可知,函数在区间端点处的函数值符号相反,解不等式求得实数a的取值范围.
解答:解:∵函数 在区间(1,2)内有零点,
在区间(1,2)内有零点,
∴f(1)•f(2)<0,
即(log33-a)•(log32-a)<0,
∴log32<a<1,
故选C.
点评:本题考查函数在某个区间存在零点的性质,若函数在某个区间内存在零点,则函数在区间端点处的函数值符号相反.
解答:解:∵函数
 在区间(1,2)内有零点,
在区间(1,2)内有零点,∴f(1)•f(2)<0,
即(log33-a)•(log32-a)<0,
∴log32<a<1,
故选C.
点评:本题考查函数在某个区间存在零点的性质,若函数在某个区间内存在零点,则函数在区间端点处的函数值符号相反.

练习册系列答案
相关题目
设函数 在区间(1,2)内有零点,则实数a的取值范围是( )
在区间(1,2)内有零点,则实数a的取值范围是( )
A. | B. | C. | D. |
 在区间(1,2)内有零点,则实数a的取值范围是( )
在区间(1,2)内有零点,则实数a的取值范围是( ) B.
B. C.
C. D.
D.
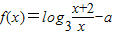 在区间(1,2)内有零点,则实数a的取值范围是 .
在区间(1,2)内有零点,则实数a的取值范围是 .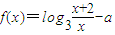 在区间(1,2)内有零点,则实数a的取值范围是( )
在区间(1,2)内有零点,则实数a的取值范围是( )