题目内容
从某年级学生中,随机抽取50人,其体重(单位:千克)的频数分布表如下:
| 分组(体重) | 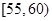 | 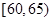 | 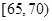 | 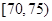 |
| 频数(人) | 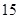 | 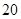 | 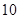 | 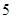 |
(1)根据频数分布表计算体重在
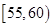 的频率;
的频率;(2)用分层抽样的方法从这50人中抽取10人,其中体重在
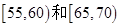 中共有几人?
中共有几人?(3)在(2)中抽出的体重在
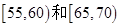 的人中,任取2人,求体重在
的人中,任取2人,求体重在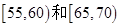 中各有1人的概率.
中各有1人的概率.
(1) ;(2)5人;(3)
;(2)5人;(3)
解析试题分析:(1)频率=频数÷样本总量;(2)分层抽样要按各层占的比例抽取,从这50人中抽取10人就确定了各层内的抽取的比例为 ,故在
,故在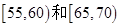 内抽取的比例也都是
内抽取的比例也都是 ,共有:
,共有: (人);(3)抽出的体重在
(人);(3)抽出的体重在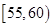 和
和 的5人中有三人体重在
的5人中有三人体重在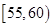 内,有2人体重在
内,有2人体重在 内,可采用列举法把所以可能的情况一一列举出,共10种情况,从中找出符合要求的情况有6中,故. 故体重在
内,可采用列举法把所以可能的情况一一列举出,共10种情况,从中找出符合要求的情况有6中,故. 故体重在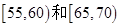 中各有1人的概率为
中各有1人的概率为 .
.
试题解析:(1)体重在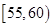 的频率
的频率
(2)用分层抽样的方法抽取10人,其中体重在体重在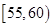 和
和 中共有:
中共有: (人)
(人)
(3)抽出的体重在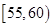 和
和 的5人中,设体重
的5人中,设体重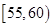 中的人为
中的人为 ,体重在
,体重在 中的人为
中的人为 ,任取2 人,共有:
,任取2 人,共有: 这10种情况.
这10种情况.
其中体重在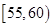 和
和 中各有1人的情况有:
中各有1人的情况有: 共6种.
共6种.
故体重在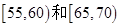 中各有1人的概率为
中各有1人的概率为 .
.
考点:1、分层抽样方法;2、古典概型.

今年年初,我国多个地区发生了持续性大规模的雾霾天气,给我们的身体健康产生了巨大的威胁。私家车的尾气排放也是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力。为此,很多城市实施了机动车车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
(2)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行进行追踪调查,记选中的4人中不赞成“车辆限行”的人数为ξ,求随机变量ξ的分布列和数学期望.
为考查某种药物预防疾病的效果,进行动物试验,得到如下丢失数据的列联表:
| | 患病 | 未患病 | 总计 |
| 没服用药 | 20 | 30 | 50 |
| 服用药 | 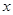 | 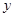 | 50 |
| 总计 | 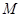 | 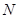 | 100 |
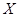 ;从服用药物的动物中任取两只,未患病数为
;从服用药物的动物中任取两只,未患病数为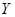 ,工作人员曾计算过
,工作人员曾计算过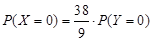 .
. (1)求出列联表中数据
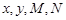 的值;
的值; (2)能够以99%的把握认为药物有效吗?参考公式:
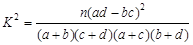 ,其中
,其中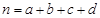 ;
;①当K2≥3.841时有95%的把握认为
 、
、 有关联;
有关联;②当K2≥6.635时有99%的把握认为
 、
、 有关联.
有关联. 据《中国新闻网》10月21日报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改”引起广泛关注.为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人调查(若所选择的在校学生的人数低于被调查人群总数的80%,则认为本次调查“失效”),就“是否取消英语听力”的问题,调查统计的结果如下表:
| 应该取消 | 应该保留 | 无所谓 | ||
| 在校学生 | 2100人 | 120人 | y人 | ||
| 社会人士 | 600人 | x人 | z人 |
(Ⅰ)现用分层抽样的方法在所有参与调查的人中抽取360人进行深入访谈,问应在持“无所谓”态度的人中抽取多少人?
(Ⅱ)已知y≥657,z≥55,求本次调查“失效”的概率.


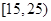 ,
,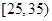 的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“车辆限行”的人数为
的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“车辆限行”的人数为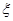 ,求随机变量
,求随机变量
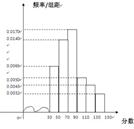
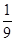 ,求甲在初赛中答题个数的分布列及数学期望.
,求甲在初赛中答题个数的分布列及数学期望.