题目内容
甲、乙两名同学参加“汉字听写大赛”选拔性测试.在相同的测试条件下,两人5次测试的成绩(单位:分)如下表:
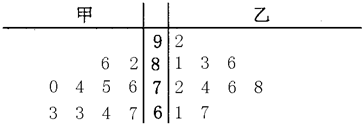
(Ⅰ)请画出甲、乙两人成绩的茎叶图. 你认为选派谁参赛更好?说明理由(不用计算);
(Ⅱ)若从甲、乙两人5次的成绩中各随机抽取一个成绩进行分析,求抽到的两个成绩中至少有一个高于
90分的概率.
(Ⅰ)略;(Ⅱ)
解析试题分析:(Ⅰ)茎表示得分的十位数,放在中间的列,叶表示得分的个位数,放在两侧。从茎叶图可观察出甲的得分比较分散,乙得分比较集中即波动小、相对稳定,所以应选派乙参赛更好。(Ⅱ)用列举法例举出所有基本事件,和抽到的两个成绩中至少有一个高于90分的基本事件,根据古典概型概率公式 求其概率。
求其概率。
试题解析:
(Ⅰ)茎叶图如下图所示,由图可知,乙的平均成绩大于甲的平均成绩,且乙的方差小于甲的方差,因此应选派乙参赛更好. 6分
(Ⅱ)设事件 :抽到的成绩中至少有一个高于90分.
:抽到的成绩中至少有一个高于90分.
从甲、乙两人5次的成绩中各随机抽取一个成绩,所有的基本事件如下:
共25个.
事件 包含的基本事件有
包含的基本事件有
共9个.
所以 ,即抽到的成绩中至少有一个高于90分的概率为
,即抽到的成绩中至少有一个高于90分的概率为 . .13分
. .13分
考点:1.茎叶图;2.古典概型

 阅读快车系列答案
阅读快车系列答案从某年级学生中,随机抽取50人,其体重(单位:千克)的频数分布表如下:
| 分组(体重) | 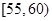 | 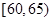 | 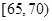 | 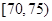 |
| 频数(人) | 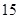 | 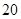 | 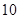 | 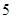 |
(1)根据频数分布表计算体重在
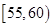 的频率;
的频率;(2)用分层抽样的方法从这50人中抽取10人,其中体重在
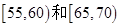 中共有几人?
中共有几人?(3)在(2)中抽出的体重在
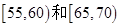 的人中,任取2人,求体重在
的人中,任取2人,求体重在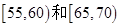 中各有1人的概率.
中各有1人的概率. 某学校餐厅新推出A,B,C,D四款套餐,某一天四款套餐销售情况的条形图如下. 为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
| | 满意 | 一般 | 不满意 |
| A套餐 | 50% | 25% | 25% |
| B套餐 | 80% | 0 | 20% |
| C套餐 | 50% | 50% | 0 |
| D套餐 | 40% | 20% | 40% |

(Ⅰ)若同学甲选择的是A款套餐,求甲的调查问卷被选中的概率;
(Ⅱ)若想从调查问卷被选中且填写不满意的同学中再选出2人进行面谈,求这两人中至少有一人选择的是D款套餐的概率.
空气质量指数 (单位:
(单位: )表示每立方米空气中可入肺颗粒物的含量,这个值越高,代表空气污染越严重.
)表示每立方米空气中可入肺颗粒物的含量,这个值越高,代表空气污染越严重. 的浓度与空气质量类别的关系如下表所示:
的浓度与空气质量类别的关系如下表所示:
 日均浓度 日均浓度 |  |  |  |  |  |  |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
 年
年 月份的
月份的 天中随机抽取
天中随机抽取 天的
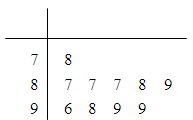
天的 日均浓度指数数据茎叶图如图5所示.
日均浓度指数数据茎叶图如图5所示.
(1)试估计甲城市在
 年
年 月份的
月份的 天的空气质量类别为优或良的天数;
天的空气质量类别为优或良的天数;(2)在甲城市这
 个监测数据中任取
个监测数据中任取 个,设
个,设 为空气质量类别为优或良的天数,求
为空气质量类别为优或良的天数,求 的分布列及数学期望.
的分布列及数学期望. 由世界自然基金会发起的“地球1小时”活动,已发展成为最有影响力的环保活动之一,今年的参与人数再创新高,然而也有部分公众对该活动的实际效果与负面影响提出了疑问,对此,某新闻媒体进行了网上调查,所有参与调查的人中,持“支持”、“保留”和“不支持”态度的人数如下表所示:
| | 支持 | 保留 | 不支持 |
| 20岁以下 | 800 | 450 | 200 |
| 20岁以上(含20岁) | 100 | 150 | 300 |
(Ⅱ)在持“不支持”态度的人中,用分层抽样的方法抽取5人看成一个总体,从这5人中任意选取2人,求至少有1人20岁以下的概率;
(Ⅲ)在接受调查的人中,有8人给这项活动打出的分数如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2,把这8个人打出的分数看作一个总体,从中任取1个数,求该数与总体平均数之差的绝对值超过0.6的概率.
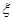 表示抽到评价该教师为
表示抽到评价该教师为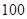 分,规定测试成绩在
分,规定测试成绩在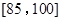 之间为体质优秀;在
之间为体质优秀;在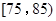 之间为体质良好;在
之间为体质良好;在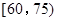 之间为体质合格;在
之间为体质合格;在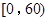 之间为体质不合格.
之间为体质不合格.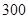 名学生中随机抽取
名学生中随机抽取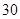 名学生体质健康测试成绩,其茎叶图如下:
名学生体质健康测试成绩,其茎叶图如下: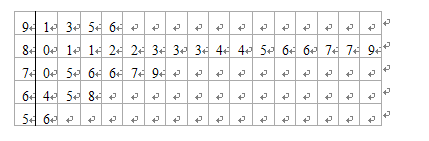
 名学生,再从这
名学生,再从这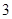 人.
人. 名体质为优秀的概率;
名体质为优秀的概率;