题目内容
某工厂有25周岁以上(含2S周岁)工人300名,25周岁以下工人200名为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:[50,60), [60,70), [70,80), [80,90), [90,100), 分别加以统计,得到如图所示的频率分布直方图。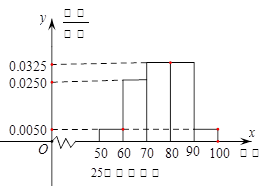
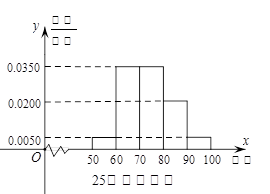
(1)求样本中“25周岁以上(含25周岁)组”抽取的人数、日生产量平均数;
(2)若“25周岁以上组”中日平均生产90件及90件以上的称为“生产能手”;“25周岁以下组”中日平均生产不足60件的称为“菜鸟”。从样本中的“生产能手”和”菜鸟”中任意抽取2人,求这2人日平均生产件数之和X的分布列及期望。(“生产能手”日平均生产件数视为95件,“菜鸟”日平均生产件数视为55件)。
(Ⅰ)样本中有 周岁以上组工人
周岁以上组工人 名,平均数为73.5;(2)
名,平均数为73.5;(2) .
.
解析试题分析:(Ⅰ)分层抽样实质上就是按比例抽样,根据比例即可求得样本中有 周岁以上组工人的人数;
周岁以上组工人的人数;
根据频率分布直方图求平均数的公式为 ,其中
,其中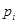 为第
为第 组数据的频率,
组数据的频率,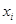 是第
是第 组数据的中间值.由此公式可得样本中“25周岁以上(含25周岁)组”的日生产量平均数.
组数据的中间值.由此公式可得样本中“25周岁以上(含25周岁)组”的日生产量平均数.
(2)首先根据频率求出样本中“ 周岁以上组”中的 “生产能手”的人数和 “25周岁以下组”中的“菜鸟”工人的人数,用字母表示这些工人,然后一一列出所有可能结果,再数出改好能组成师徒组的可能结果,由古典概型概率公式求得所求概率.
周岁以上组”中的 “生产能手”的人数和 “25周岁以下组”中的“菜鸟”工人的人数,用字母表示这些工人,然后一一列出所有可能结果,再数出改好能组成师徒组的可能结果,由古典概型概率公式求得所求概率.
试题解析:(Ⅰ)由已知得,样本中有 周岁以上组工人
周岁以上组工人
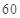 名 4分
名 4分
样本中“25周岁以上(含25周岁)组”的日生产量平均数为 5分
5分
(2)由样本中“ 周岁以上组”中日平均生产90件及90件以上的 “生产能手”工人有
周岁以上组”中日平均生产90件及90件以上的 “生产能手”工人有 (人), 记为
(人), 记为 .“25周岁以下组”中日平均生产不足60件的称为“菜鸟”工人有
.“25周岁以下组”中日平均生产不足60件的称为“菜鸟”工人有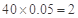 (人),记为
(人),记为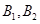 . 8分
. 8分
从中随机地抽取两人,所有可能的结果共有以下10种: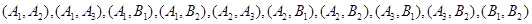 10分
10分
其中,2人恰好能组成师徒组的可能结果共有以下6种: .
.
由古典概型的概率公式得所求概率为: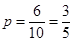 12分
12分
考点:1、频率分布直方图;2、古典概型.

 阅读快车系列答案
阅读快车系列答案某高校在2013年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示.
| 组号 | 分组 | 频数 | 频率 |
| 第1组 |  | 5 | 0.050 |
| 第2组 | 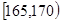 | ① | 0.350 |
| 第3组 |  | 30 | ② |
| 第4组 | 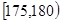 | 20 | 0.200 |
| 第5组 | 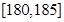 | 10 | 0.100 |
| 合计 | 100 | 1.00 | |
(1)请先求出频率分布表中①、②位置相应的数据,再在答题卷上完成下列频率分布直方图;

(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行面试,求:第4组至少有一名学生被考官A面试的概率?
从某年级学生中,随机抽取50人,其体重(单位:千克)的频数分布表如下:
| 分组(体重) | 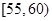 | 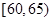 | 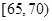 | 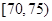 |
| 频数(人) | 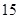 | 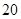 | 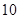 | 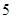 |
(1)根据频数分布表计算体重在
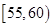 的频率;
的频率;(2)用分层抽样的方法从这50人中抽取10人,其中体重在
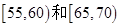 中共有几人?
中共有几人?(3)在(2)中抽出的体重在
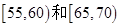 的人中,任取2人,求体重在
的人中,任取2人,求体重在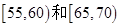 中各有1人的概率.
中各有1人的概率. 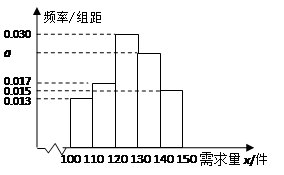
 的值,并估计日需求量的众数;
的值,并估计日需求量的众数; 件能获利30元,未售出的部分,每件亏损20元.设当天的需求量为
件能获利30元,未售出的部分,每件亏损20元.设当天的需求量为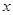 件(
件( ),纯利润为
),纯利润为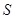 元.
元. 元的概率.
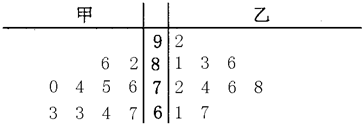
元的概率. 名同学,现测得排球队
名同学,现测得排球队 )分别是:
)分别是: 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、

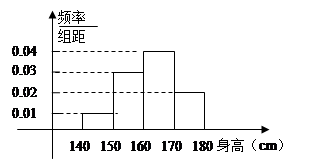
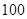 户家庭,分别调查了他们在政府动员前后三个月的月平均用水量(单位:吨),将所得数据分组,画出频率分布直方图(如图所示)
户家庭,分别调查了他们在政府动员前后三个月的月平均用水量(单位:吨),将所得数据分组,画出频率分布直方图(如图所示)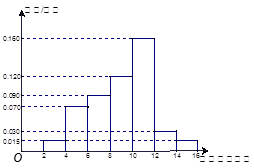
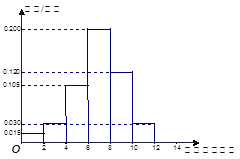
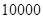 户,在政府进行节水动员前平均每月用水量是
户,在政府进行节水动员前平均每月用水量是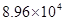 吨,请估计该小区在政府动员后比动员前平均每月节约用水多少吨;
吨,请估计该小区在政府动员后比动员前平均每月节约用水多少吨;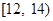 内的家庭中选出
内的家庭中选出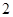 户作为采访对象,其中甲、乙两家在备选之列,求恰好选中他们两家作为采访对象的概率
户作为采访对象,其中甲、乙两家在备选之列,求恰好选中他们两家作为采访对象的概率