题目内容
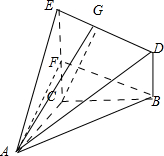
已知几何体A-BCED的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.

(1)求此几何体的体积V的大小;
(2)求异面直线DE与AB所成角的余弦值;
(3)求二面角A-ED-B的正弦值.

(1)求此几何体的体积V的大小;
(2)求异面直线DE与AB所成角的余弦值;
(3)求二面角A-ED-B的正弦值.
考点:异面直线及其所成的角,棱柱、棱锥、棱台的体积,二面角的平面角及求法
专题:计算题
分析:(1)通过已知条件可知,AC⊥底面BCED,再求出梯形BCED的面积,根据三棱锥的体积公式即可求出体积.
(2)先找到异面直线所成的角,可过B作DE的平行线,则角ABF便是异面直线所成的角,根据条件求出即可.
(3)先找出二面角的平面角,过C作CG⊥ED,并交ED于G,连接AG,则∠AGC即是所找的二面角的平面角,根据条件求出即可.
(2)先找到异面直线所成的角,可过B作DE的平行线,则角ABF便是异面直线所成的角,根据条件求出即可.
(3)先找出二面角的平面角,过C作CG⊥ED,并交ED于G,连接AG,则∠AGC即是所找的二面角的平面角,根据条件求出即可.
解答:
 解:(1)∵∠ACE,∠ACB都是直角,∴AC⊥BC,AC⊥CE,CB∩CE=C,CB?平面BCED,CE?平面BCED;
解:(1)∵∠ACE,∠ACB都是直角,∴AC⊥BC,AC⊥CE,CB∩CE=C,CB?平面BCED,CE?平面BCED;
∴AC⊥平面BCED.
∴V=
SBCED•AC=
×12×4=16.
(2)取CE中点F,连接BF,则BF∥DE,则∠ABF即异面直线DE与AB所成的角,连接AF.
在△ABF中,AB=4
,BF=2
,AF=2
;
∴由余弦定理得:cos∠ABF=
=
=
;
异面直线DE与AB所成角的余弦值是
.
(3)过C作CG⊥DE,交DE于G,连接AG,∵AC⊥平面BCED,ED?平面BCED,∴AC⊥ED;
∴ED⊥平面ACG,AG?平面ACG,∴ED⊥AG,∴∠AGC是二面角A-ED-B的平面角;
在Rt△ACG中,AC=4,CG=4×
=
,∠ACG=90°;
∴tan∠AGC=
=
,sin∠AGC=
.
 解:(1)∵∠ACE,∠ACB都是直角,∴AC⊥BC,AC⊥CE,CB∩CE=C,CB?平面BCED,CE?平面BCED;
解:(1)∵∠ACE,∠ACB都是直角,∴AC⊥BC,AC⊥CE,CB∩CE=C,CB?平面BCED,CE?平面BCED;∴AC⊥平面BCED.
∴V=
| 1 |
| 3 |
| 1 |
| 3 |
(2)取CE中点F,连接BF,则BF∥DE,则∠ABF即异面直线DE与AB所成的角,连接AF.
在△ABF中,AB=4
| 2 |
| 5 |
| 5 |
∴由余弦定理得:cos∠ABF=
| BF2+AB2-AF2 |
| 2BF•AB |
| 20+32-20 | ||||
2×2
|
| ||
| 5 |
异面直线DE与AB所成角的余弦值是
| ||
| 5 |
(3)过C作CG⊥DE,交DE于G,连接AG,∵AC⊥平面BCED,ED?平面BCED,∴AC⊥ED;
∴ED⊥平面ACG,AG?平面ACG,∴ED⊥AG,∴∠AGC是二面角A-ED-B的平面角;
在Rt△ACG中,AC=4,CG=4×
| 4 | ||
|
8
| ||
| 5 |
∴tan∠AGC=
| 4 | ||||
|
| ||
| 2 |
| ||
| 3 |
点评:求异面直线所成角时,通过作另一直线的平行线,找出这个角,然后把它放在一个三角形里去求即可.求二面角时,先找到二面角的平面角,然后把它放在一个三角形里去求即可.

练习册系列答案
相关题目
已知函数f(x)=
,(a>0,且a≠1),若数列{an}满足an=f(n),(n∈N+),且{an}是递增数列,则实数a的取值范围是( )
|
| A、(0,1) | ||
B、[
| ||
| C、(1,3) | ||
| D、(2,3) |
椭圆
+
=1短轴的一个端点与两个焦点构成一个等边三角形,则椭圆离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 在一个边长为100cm的正方形ABCD中,以A为圆心半径为90cm做一四分之一圆,分别与AB,AD相交,在圆弧上取一点P,PE垂直BC于E点,PF垂直CD于F点.
在一个边长为100cm的正方形ABCD中,以A为圆心半径为90cm做一四分之一圆,分别与AB,AD相交,在圆弧上取一点P,PE垂直BC于E点,PF垂直CD于F点.