题目内容
已知双曲线C : -
- =1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为( )
=1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为( )
A. - - =1 =1 | B. - - =1 =1 | C. - - =1 =1 | D. - - =1 =1 |
A.
解析试题分析:因为双曲线C : -
- =1的焦距为10,所以2c=10,即c=5.所以焦点坐标为F1
=1的焦距为10,所以2c=10,即c=5.所以焦点坐标为F1 和F2
和F2 ,由双曲线的定义得:2a=
,由双曲线的定义得:2a= =4
=4 ,即a=
,即a= ,所以b=
,所以b= ,所以C的方程为
,所以C的方程为 -
- =1。
=1。
考点:本题考查双曲线的定义和简单性质。
点评:在做题时很多同学误认为焦距为c,导致出错。实际上焦距是2c,实轴长为2a,虚轴长为2b。

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
若方程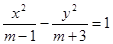 表示双曲线,则实数
表示双曲线,则实数 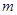 的取值范围是 ( )
的取值范围是 ( )
A. | B. |
C.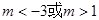 | D. |
已知曲线C: 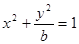 与抛物线
与抛物线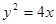 的一个交点为M,
的一个交点为M,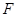 为抛物线的焦点,若
为抛物线的焦点,若 ,则b的值为
,则b的值为
A.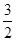 | B.-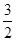 | C. | D.- |
抛物线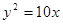 的焦点到准线的距离是
的焦点到准线的距离是
A.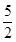 | B.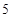 | C.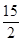 | D.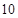 |
已知抛物线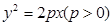 的焦点弦
的焦点弦 坐标分别为
坐标分别为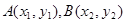 ,则
,则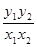 的值一定等于( )
的值一定等于( )
A.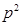 | B. | C. | D. |
抛物线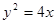 上一点
上一点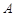 的横坐标为4,则点
的横坐标为4,则点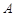 与抛物线焦点的距离为
与抛物线焦点的距离为
| A.2 | B.3 | C.4 | D.5 |
抛物线  的准线方程是( ).
的准线方程是( ).
A.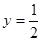 | B. | C.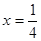 | D.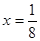 |
过双曲线 的右焦点
的右焦点 作圆
作圆 的切线
的切线 (切点为
(切点为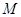 ),交
),交 轴于点
轴于点 . 若
. 若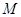 为线段
为线段 的中点,则双曲线的离心率是
的中点,则双曲线的离心率是
| A.2 | B. | C. | D. |
已知抛物线 ,过点
,过点 )作倾斜角为
)作倾斜角为 的直线
的直线 ,若
,若 与抛物线交于
与抛物线交于 、
、 两点,弦
两点,弦 的中点
的中点 到y轴的距离为( )
到y轴的距离为( )
A. | B. | C. | D. |