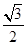题目内容
已知抛物线 ,过点
,过点 )作倾斜角为
)作倾斜角为 的直线
的直线 ,若
,若 与抛物线交于
与抛物线交于 、
、 两点,弦
两点,弦 的中点
的中点 到y轴的距离为( )
到y轴的距离为( )
A. | B. | C. | D. |
A
解析试题分析:设
 ,由直线
,由直线 与
与 联立消y得,
联立消y得, 则
则 ,弦
,弦 的中点
的中点 到y轴的距离为
到y轴的距离为 .
.
考点:直线与抛物线的位置关系,一元二次方程的根与系数的关系.
点评:本小题属于直线与抛物线的位置关系的题目,应将两方程联立,借助韦达定理求出中点P的坐标,从而可得点P到y轴的距离.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
已知双曲线C : -
- =1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为( )
=1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为( )
A. - - =1 =1 | B. - - =1 =1 | C. - - =1 =1 | D. - - =1 =1 |
平面内有一长度为2的线段 和一动点
和一动点 ,若满足
,若满足 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
椭圆的中心在原点,焦点在 轴上,长轴长为4,短轴长为2,则椭圆方程是( )
轴上,长轴长为4,短轴长为2,则椭圆方程是( )
A. | B. | C. | D. |
双曲线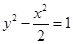 的渐近线方程为( )
的渐近线方程为( )
A.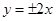 | B.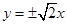 | C.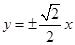 | D.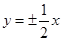 |
椭圆 与双曲线
与双曲线 有相同的焦点,则
有相同的焦点,则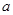 的值是 ( )
的值是 ( )
A. | B.1或–2 | C.1或 | D.1 |
椭圆 +
+ =1的离心率为( )
=1的离心率为( )
A. | B. |
C. | D. |
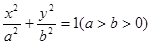 的左、右焦点,A和B是以O(O为坐标原点)为圆心,以|OF1|为半径的圆与该椭圆的两个交点,且△F2AB是等边三角形,则椭圆的离心率为( )
的左、右焦点,A和B是以O(O为坐标原点)为圆心,以|OF1|为半径的圆与该椭圆的两个交点,且△F2AB是等边三角形,则椭圆的离心率为( )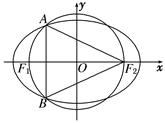
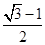
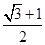
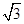 -1
-1