题目内容
5．设$\overrightarrow{a}$，$\overrightarrow{b}$为两个相互垂直的单位向量，是否存在整数k，使向量$\overrightarrow{m}$=k$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{n}$=$\overrightarrow{a}$+k$\overrightarrow{b}$的夹角为60°，若存在，求k值，若不存在，说明理由．分析 由题意利用两个向量垂直的性质可得$\overrightarrow{a}•\overrightarrow{b}$=0，再利用两个向量的数量积的运算可得 $\sqrt{{k}^{2}+1}$•$\sqrt{{k}^{2}+1}$•cos60°=2k，由此求得k的值，从而得出结论．
解答 解：由题意可得$\overrightarrow{a}•\overrightarrow{b}$=0，设向量$\overrightarrow{m}$=k$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{n}$=$\overrightarrow{a}$+k$\overrightarrow{b}$的夹角为60°，
∵|$\overrightarrow{m}$|=$\sqrt{{（k\overrightarrow{a}+\overrightarrow{b}）}^{2}}$=$\sqrt{{k}^{2}+1}$，|$\overrightarrow{n}$|=$\sqrt{{（a+k\overrightarrow{b}）}^{2}}$=$\sqrt{{k}^{2}+1}$，$\overrightarrow{m}•\overrightarrow{n}$=（k$\overrightarrow{a}$+$\overrightarrow{b}$）•（$\overrightarrow{a}$+k$\overrightarrow{b}$）=k+k=2k，
∴$\overrightarrow{m}•\overrightarrow{n}$=$\sqrt{{k}^{2}+1}$•$\sqrt{{k}^{2}+1}$•cos60°=$\frac{{k}^{2}+1}{2}$=2k，求得k=2+$\sqrt{3}$或k=2-$\sqrt{3}$．
故存在k，满足条件．
点评 本题主要考查两个向量垂直的性质，两个向量的数量积的运算，属于基础题．
期末宝典单元检测分类复习卷系列答案| A． | $\frac{1}{2}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{2}$-1 | D． | $\frac{π}{4}$-$\frac{1}{2}$ |
| A． | -$\frac{1}{3}$ | B． | $\frac{1}{3}$ | C． | ±$\frac{1}{3}$ | D． | ±$\frac{1}{2}$ |
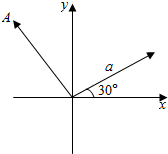如图，点A的坐标为（-2，3），向量$\overrightarrow{a}$的模为4，则向量$\overrightarrow{OA}$的坐标为（-2，3），向量$\overrightarrow{a}$的坐标为（2$\sqrt{3}$，2）．