Question

【题目】已知椭圆，圆，圆：，椭圆C与圆C1、圆C2均相切．

（1）求椭圆C的方程；

（2）直线l与圆C1相切同时与椭圆C交于A、B两点，求|AB|的最大值.

Answer 1

【答案】（1）；（2）．

【解析】

（1）由椭圆C与圆C1、圆C2均相切，可得出椭圆的与圆C1、圆C2半径的关系，进而求出椭圆C的方程；

（2）假设直线l方程，由直线方程与椭圆C方程联立，计算出弦长|AB|，根据直线与圆相切需满足的条件进一步求出|AB|的最大值.

（1）由题易知的半径，圆的半径．

又椭圆与同时相切，则，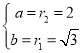

则椭圆C的方程：．

（2）①当斜率为0时，与椭圆相切，不符合题意．

②当斜率不为0时，设：，

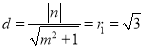原点到的距离，即.

由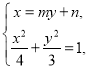

可得：，

设，由韦达定理得：

，，

，

可得，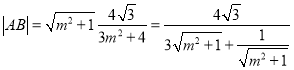

令，则，

=3t+在上单调递增，

则，即时，．