题目内容
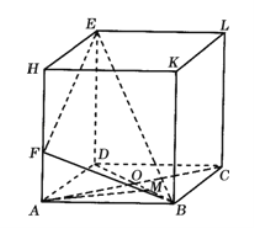
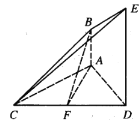
【题目】在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() 平面ABCD,E为PD的中点,
平面ABCD,E为PD的中点,![]() .
.
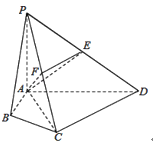
(1)求四棱锥![]() 的体积V;
的体积V;
(2)若F为PC的中点,求证:平面![]() 平面AEF;
平面AEF;
(3)求二面角![]() 的大小.
的大小.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】
(1)直接利用锥体的体积公式计算得到答案.
(2)证明![]() 平面PAC,
平面PAC,![]() ,得到
,得到![]() 平面PAC,得到证明.
平面PAC,得到证明.
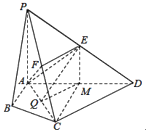
(3)取AD的中点M,连接EM,则![]() ,过M作
,过M作![]() 于Q,连接EQ,则
于Q,连接EQ,则![]() 为二面角
为二面角![]() 的平面角,计算角度得到答案.
的平面角,计算角度得到答案.
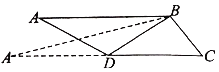
(1)在![]() 中,
中,![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() .
.
则![]() .
.
(2)∵![]() 平面ABCD,∴
平面ABCD,∴![]() ,又
,又![]() ,
,![]() ,
,
∴![]() 平面PAC,
平面PAC,
∵E、F分别为PD、PC中点,∴![]() ,∴
,∴![]() 平面PAC,
平面PAC,
∵![]() 平面AEF,∴平面
平面AEF,∴平面![]() 平面AEF.
平面AEF.
(3)取AD的中点M,连接EM,则![]() ,∴
,∴![]() 平面ACD,
平面ACD,
过M作![]() 于Q,连接EQ,则
于Q,连接EQ,则![]() 为二面角
为二面角![]() 的平面角.
的平面角.
∵M为AD的中点,![]() ,
,![]() ,
,
∴![]() ,又
,又![]() ,
,
∴![]() ,故
,故![]() .
.
即二面角![]() 的大小为30°.
的大小为30°.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目