题目内容
【题目】已知无穷数列![]() 满足:
满足:![]() ,
,![]() .
.
(Ⅰ)若![]() ;
;
(ⅰ)求证:![]() ;
;
(ⅱ)数列![]() 的前
的前![]() 项和为
项和为![]() 且
且![]() ,求证:
,求证:![]() ;
;
(Ⅱ)若对任意的![]() ,都有
,都有![]() ,写出
,写出![]() 的取值范围并说明理由.
的取值范围并说明理由.
【答案】(Ⅰ)(ⅰ)见解析;(ⅱ)见解析(Ⅱ)![]() ,见解析
,见解析
【解析】
(Ⅰ)(ⅰ)首先根据已知条件推出![]() 与
与![]() 的大小关系,计算出
的大小关系,计算出![]() ,然后求出
,然后求出![]() 的取值范围,从而可使问题得证;(ⅱ)首先根据条件求出
的取值范围,从而可使问题得证;(ⅱ)首先根据条件求出![]() ,然后求出
,然后求出![]() ,从而结合(ⅰ)的结论使问题得证;
,从而结合(ⅰ)的结论使问题得证;
(Ⅱ)首先分![]() ,
,![]() ,
,![]() 三种情况求出
三种情况求出![]() 的取值范围,然后当
的取值范围,然后当![]() 时,求出
时,求出![]() 的取值范围,从而可推出在
的取值范围,从而可推出在![]() 时,当
时,当![]() 时,
时,![]() ,不符合题意,即可求解
,不符合题意,即可求解![]() 的取值范围.
的取值范围.
(Ⅰ)证明:(ⅰ)![]() ,
,
①![]() ,∵
,∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
②假设![]() 时,
时,![]() ,则
,则![]() ,
,
∴![]() 时,
时,![]() ,
,![]() ,
,
由①②对一切正整数![]() 都有
都有![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
但当![]() 时,
时,![]() ,
,
∴![]() .
.
(ⅱ)∵![]() ,
,
∴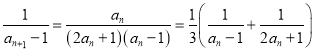 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
由(ⅰ)知![]() ,
,
∴![]() .
.
(Ⅱ)∵对任意的![]() ,都有
,都有![]() ,
,
且![]() ,∴显然
,∴显然![]() ,由(I)证明知,
,由(I)证明知,
①若![]() ,则
,则![]() ,∴
,∴![]() ,∴
,∴![]() ;
;
②若![]() ,则
,则![]() 为常数列,∴
为常数列,∴![]() ;
;
③若![]() ,则
,则![]() ,∴
,∴![]() ,
,
又![]() ,
,
若![]() ,则
,则![]() ,则
,则![]() ,
,
∴![]() ,
,
∴当![]() 时,有
时,有![]() ,
,
∴当![]() 时,
时,![]() ,不符合题意.
,不符合题意.
综上可知,![]() 。
。

 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案【题目】绿水青山就是金山银山.某山村为做好水土保持,退耕还林,在本村的山坡上种植水果,并推出山村游等旅游项目.为预估今年7月份游客购买水果的情况,随机抽样统计了去年7月份100名游客的购买金额.分组如下:![]() ,
,![]() ,
,![]()
![]() ,得到如图所示的频率分布直方图:
,得到如图所示的频率分布直方图:
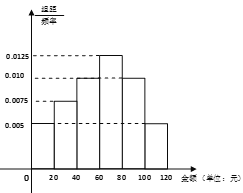
(1)请用抽样的数据估计今年7月份游客人均购买水果的金额(同一组中的数据用该组区间中点作代表).
(2)若把去年7月份购买水果不低于80元的游客,称为“水果达人”. 填写下面列联表,并根据列联表判断是否有95%的把握认为“水果达人”与性别有关系?
水果达人 | 非水果达人 | 合计 | |
男 | 10 | ||
女 | 30 | ||
合计 |
(3)为吸引顾客,商家特推出两种促销方案.方案一:每满80元可立减10元;方案二:金额超过80元可抽奖三次,每次中奖的概率为![]() ,且每次抽奖互不影响,中奖1次打9折,中奖2次打8折,中奖3次打7折.若每斤水果10元,你打算购买12斤水果,请从实际付款金额的数学期望的角度分析应该选择哪种优惠方案.
,且每次抽奖互不影响,中奖1次打9折,中奖2次打8折,中奖3次打7折.若每斤水果10元,你打算购买12斤水果,请从实际付款金额的数学期望的角度分析应该选择哪种优惠方案.
附:参考公式和数据:![]() ,
,![]() .临界值表:
.临界值表:
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |
【题目】在传染病学中,通常把从致病刺激物侵入机体或者对机体发生作用起,到机体出现反应或开始呈现该疾病对应的相关症状时止的这一阶段称为潜伏期.一研究团队统计了某地区200名患者的相关信息,得到如下表格:
潜伏期(单位:天) |
|
|
|
|
|
|
|
人数 | 17 | 41 | 62 | 50 | 26 | 3 | 1 |
(1)求这200名患者的潜伏期的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)该传染病的潜伏期受诸多因素的影响,为研究潜伏期与患者年龄的关系,以潜伏期是否超过6天为标准进行分层抽样,从上述200名患者中抽取40人得到如下列联表.请将列联表补充完整,并根据列联表判断是否有95%的把握认为潜伏期与患者年龄有关;
潜伏期 | 潜伏期 | 总计 | |
50岁以上(含50岁) | 20 | ||
50岁以下 | 9 | ||
总计 | 40 |
(3)以这200名患者的潜伏期超过6天的频率,代替该地区1名患者潜伏期超过6天发生的概率,每名患者的潜伏期是否超过6天相互独立.为了深入硏究,该研究团队在该地区随机调查了10名患者,其中潜伏期超过6天的人数最有可能(即概率最大)是多少?
附:
| 0.05 | 0.025 | 0.010 |
| 3.841 | 5.024 | 6.635 |
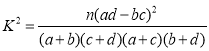 ,其中
,其中![]()