题目内容
以y轴为准线的椭圆经过定点M(1,2),且离心率e=| 1 | 2 |
分析:设椭圆的左焦点为F(x,y),依据椭圆的统一定义,建立关于x,y的关系式,化简即得左焦点的轨迹方程.
解答:解:设椭圆的左焦点为F(x,y).
由椭圆的定义得
=
∴
=
化简得:(x-1)2+(y-2)2=
.
故填:(x-1)2+(y-2)2=
.
由椭圆的定义得
| MF |
| d |
| 1 |
| 2 |
∴
| ||
| 1 |
| 1 |
| 2 |
化简得:(x-1)2+(y-2)2=
| 1 |
| 2 |
故填:(x-1)2+(y-2)2=
| 1 |
| 2 |
点评:本题主要考查求轨迹方程,解决与椭圆有关的轨迹问题时,要充分考虑到椭圆的几何性质,这样会使问题的解决简便些.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
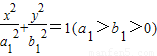 与双曲线
与双曲线 共焦点,点P是该椭圆与双曲线在第一象限的公共点,如果以椭圆的右焦点为焦点,以y轴为准线的抛物线恰过P点,那么椭圆的离心率e1与双曲线的离心率e2之间的关系为( )
共焦点,点P是该椭圆与双曲线在第一象限的公共点,如果以椭圆的右焦点为焦点,以y轴为准线的抛物线恰过P点,那么椭圆的离心率e1与双曲线的离心率e2之间的关系为( )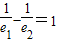
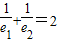
 ,则椭圆的左焦点的轨迹方程为 .
,则椭圆的左焦点的轨迹方程为 .