题目内容
【题目】已知圆![]() :
: ![]() ,直线
,直线![]() 过定点
过定点![]() .
.
(Ⅰ)若![]() 与圆
与圆![]() 相切,求
相切,求![]() 的方程;
的方程;
(Ⅱ)若![]() 与圆
与圆![]() 相交于
相交于![]() 、
、![]() 两点,求
两点,求![]() 的面积的最大值,并求此时直线
的面积的最大值,并求此时直线![]() 的方程.(其中点
的方程.(其中点![]() 是圆
是圆![]() 的圆心)
的圆心)
【答案】(Ⅰ)x=1或3x-4y=3;(Ⅱ) ![]() 最大为2.
最大为2.
【解析】试题分析:
(Ⅰ)分类讨论:
直线![]() 无斜率时,直线
无斜率时,直线![]() 的方程为
的方程为![]() ,此时直线
,此时直线![]() 和圆
和圆![]() 相切,
相切,
直线![]() 有斜率时,结合圆心到直线的距离等于半径得到关于k的方程,解方程可得
有斜率时,结合圆心到直线的距离等于半径得到关于k的方程,解方程可得![]() ,则直线方程为
,则直线方程为![]() ,
,
综上可得直线方程为x=1或3x-4y=3.
(Ⅱ)结合三角形面积公式可知,当![]() ,面积有最大值
,面积有最大值![]() ,
,
由几何关系可知圆心到直线的距离为![]() ,利用点到直线距离公式可知直线的斜率
,利用点到直线距离公式可知直线的斜率![]() 或1,则直线方程为:
或1,则直线方程为: ![]() .
.
试题解析:
(Ⅰ)直线![]() 无斜率时,直线
无斜率时,直线![]() 的方程为
的方程为![]() ,此时直线
,此时直线![]() 和圆
和圆![]() 相切,
相切,
直线![]() 有斜率时,设方程为
有斜率时,设方程为![]() ,利用圆心到直线的距离等于半径得:
,利用圆心到直线的距离等于半径得: ![]() ,直线方程为
,直线方程为![]() ,
,
故所求直线方程为x=1或3x-4y=3.
(Ⅱ)![]() 面积最大时,
面积最大时, ![]() ,
, ![]() ,
,
即![]() 是等腰直角三角形,由半径
是等腰直角三角形,由半径![]() 得:圆心到直线的距离为
得:圆心到直线的距离为![]() ,
,
设直线![]() 的方程为:
的方程为: ![]() 或1,
或1,
直线方程为: ![]() .
.

 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案【题目】如图,在直角坐标系![]() 中,椭圆
中,椭圆![]() 的上焦点为
的上焦点为![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点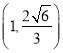 .
.
(1)求椭圆![]() 的方程.
的方程.
(2)设过椭圆![]() 的上顶点
的上顶点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
【题目】某P2P平台需要了解该平台投资者的大致年龄分布,发现其投资者年龄大多集中在区间[20,50]岁之间,对区间[20,50]岁的人群随机抽取20人进行了一次理财习惯调查,得到如下统计表和各年龄段人数频率分布直方图:
组数 | 分组 | 人数(单位:人) |
第一组 | [20,25) | 2 |
第二组 | [25,30) | a |
第三组 | [30,35) | 5 |
第四组 | [35,40) | 4 |
第五组 | [40,45) | 3 |
第六组 | [45,50] | 2 |

(Ⅰ)求a的值并画出频率分布直方图;
(Ⅱ)在统计表的第五与第六组的5人中,随机选取2人,求这2人的年龄都小于45岁的概率.