题目内容
【题目】某海轮以每小时30海里的速度航行,在点![]() 测得海面上油井
测得海面上油井![]() 在南偏东
在南偏东![]() ,海轮向北航行40分钟后到达点
,海轮向北航行40分钟后到达点![]() ,测得油井
,测得油井![]() 在南偏东
在南偏东![]() ,海轮改为北偏东
,海轮改为北偏东![]() 的航向再行驶80分钟到达点
的航向再行驶80分钟到达点![]() ,则
,则![]() 两点的距离为(单位:海里)
两点的距离为(单位:海里)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】分析:由题意可得△PBC为直角三角形,其中∠PBC=90°,BC易求,所以要求PC转求PB,解△PAB需构造直角三角形,因此过P作AB的垂线.
详解:过P作AB的垂线,垂足为E,
由题意得∠APB=∠ABP=30°.
∴AP=AB=30×![]() =20.
=20.
在Rt△PAE中,PE=APsin60°=10![]() ,
,
在Rt△PBE中,PB=![]() =20
=20![]() ,
,
由已知可得∠PBC=90°,BC=30×![]() =40,
=40,
∴Rt△PBC中,PC=![]() =20
=20![]() (海里).
(海里).

点晴:本题考查的内容为解三角形问题的实际应用,注重正余弦定理的应用,正确画出草图,标上已知的边和选,选用正确的公式

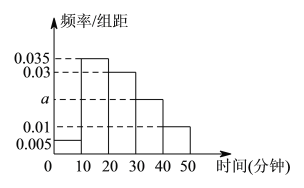
【题目】某市电力公司为了制定节电方案,需要了解居民用电情况,通过随机抽样,电力公司获得了![]() 户居民的月平均用电量,分为六组制出频率分布表和频率分布直方图(如图所示).
户居民的月平均用电量,分为六组制出频率分布表和频率分布直方图(如图所示).
组号 | 分组 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

(1)求![]() ,
, ![]() 的值;
的值;
(2)为了解用电量较大的用户用电情况,在第![]() 、
、![]() 两组用分层抽样的方法选取
两组用分层抽样的方法选取![]() 户.
户.
①求第![]() 、
、![]() 两组各取多少户?
两组各取多少户?
②若再从这![]() 户中随机选出
户中随机选出![]() 户进行入户了解用电情况,求这
户进行入户了解用电情况,求这![]() 户中至少有一户月平均用电量在
户中至少有一户月平均用电量在![]() 范围内的概率.
范围内的概率.
【题目】天气预报说,在今后的三天中,每一天下雨的概率均为40%,现部门通过设计模拟实验的方法研究三天中恰有两天下雨的概率:先利用计算器产生0到9之间取整数值的随机数,用1,2,3,4表示下雨,其余6个数字表示不下雨:产生了20组随机数:
907 | 966 | 191 | 925 | 271 | 932 | 812 | 458 | 569 | 683 |
431 | 257 | 393 | 027 | 556 | 488 | 730 | 113 | 537 | 989 |
则这三天中恰有两天降雨的概率约为__________.