题目内容

3．设数列{an}是单调递增的等差数列，a1=2且a1-1，a3，a5+5成等比数列，则a2017=（　　）
A．1008B．1010C．2016D．2017

分析 利用等差数列通项公式、等比数列性质列出方程，求出公差，由此能求出结果．

解答 解：∵数列{an}是单调递增的等差数列，
a1=2且a1-1，a3，a5+5成等比数列，
∴${{a}_{3}}^{2}=（{a}_{1}-1）（{a}_{5}+5）$，
（2+2d）2=（2-1）（2+4d+5），
解得d=-$\frac{3}{2}$（舍）或d=$\frac{1}{2}$，
∴a2017=2+2016×（$\frac{1}{2}$）=1010．
故选：B．

点评 本题考查等差数列的第2017项的求法，是基础题，解题时要认真审题，注意等差数列、等比数列的性质的合理运用．

练习册系列答案
相关题目
13．若实数x，y满足x2+y2-2y=0，且（k-1）x-y-3k+5≤0恒成立，则实数k的取值范围为k≥$\frac{7}{4}$．
14．已知m为实数，i为虚数单位，若m+（m2-4）i＞0，则$\frac{m+2i}{2-2i}$=（　　）
A．iB．1C．-iD．-1
11．过函数$f（x）=\frac{1}{3}{x^3}-{x^2}$图象上一个动点作函数的切线，则切线倾斜角的范围为（　　）
A．$[0，\frac{3π}{4}]$B．$[0，\frac{π}{2}）∪[\frac{3π}{4}，π）$C．$[\frac{3π}{4}，π）$D．$（\frac{π}{2}，\frac{3π}{4}]$
18．在平面直角坐标系中，以坐标原点为极点，x轴的非负半轴为极轴建立极坐标系．已知曲线C1：ρ=cosθ-sinθ，曲线${C_2}：\left\{{\begin{array}{l}{x=\frac{1}{2}-\frac{{\sqrt{2}}}{2}t}\\{y=\frac{{\sqrt{2}}}{2}t}\end{array}}\right.$（t为参数）．
（1）求曲线C1的直角坐标方程；
（2）若曲线C1与曲线C2相交于P、Q两点，求|PQ|的值．
8．在直角坐标系xOy中，曲线${C_1}：\left\{\begin{array}{l}x=1+2t\\ y=2-2t\end{array}\right.$（t为参数，t∈R），曲线${C_2}：\left\{\begin{array}{l}x=2cosθ+2\\ y=2sinθ\end{array}\right.$（θ为参数，θ∈[0，2π]）．
（Ⅰ）以O为极点，x轴正半轴为极轴，取相同的长度单位建立极坐标系，求曲线C2的极坐标方程；
（Ⅱ）若曲线C1与曲线C2相交于点A、B，求|AB|．
15．已知集合M={x|x≥-1}，N={x|-2＜x＜2}，则M∩N=（　　）
A．（-∞，-1]B．[-1，2）C．（-1，2]D．（2，+∞）
12．圆x2+y2-4x+6y=0的圆心坐标是（　　）
A．（2，3）B．（-2，3）C．（-2，-3）D．（2，-3）
13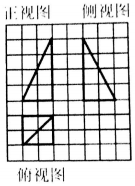．如图所示，网格纸上小正方形的边长为1，粗线画出的是某一几何体的三视图，则该几何体外接球的表面积为（　　）
A．8πB．16πC．20πD．24π

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网