题目内容
△ABC中，AB=6，AC=4，当∠A变化时，求∠A的平分线与BC的垂直平分线的交点P的轨迹．
考点：轨迹方程
专题：直线与圆
分析：取A为极点，AB所在直线为极轴建立极坐标系，分别在三角形PAC和PAB中，由余弦定理得到PC2，PB2的值，由PB=PC得到P点的极坐标方程，化为直角坐标方程得答案．
解答：
解：取A为极点，AB所在直线为极轴建立极坐标系，
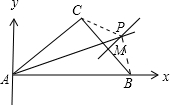
∵AP平分∠BAC，MP为BC的中垂线，
∴PB=PC，设P（ρ，θ）（ρ＞0，-
＜θ＜
且θ≠0），
则PC2=AP2+AC2-2AP•AC•cosθ=ρ2+16-8ρcosθ，
PB2=AP2+AB2-2AP•AB•cosθ=ρ2+36-12ρcosθ，
∴ρ2+16-8ρcosθ=ρ2+36-12ρcosθ．
即ρcosθ=5 （ρ＞0，-
＜θ＜
且θ≠0），
化为普通方程为x=5（y≠0）．
∴点P的轨迹是与AB垂直，且与A的距离为5的一条直线，除去垂足．
∵AP平分∠BAC，MP为BC的中垂线，
∴PB=PC，设P（ρ，θ）（ρ＞0，-
| π |
| 2 |
| π |
| 2 |
则PC2=AP2+AC2-2AP•AC•cosθ=ρ2+16-8ρcosθ，
PB2=AP2+AB2-2AP•AB•cosθ=ρ2+36-12ρcosθ，
∴ρ2+16-8ρcosθ=ρ2+36-12ρcosθ．
即ρcosθ=5 （ρ＞0，-
| π |
| 2 |
| π |
| 2 |
化为普通方程为x=5（y≠0）．
∴点P的轨迹是与AB垂直，且与A的距离为5的一条直线，除去垂足．
点评：本题考查了轨迹方程，训练了极坐标与直角坐标的互化，考查了余弦定理的应用，是中档题．
练习册系列答案
相关题目
已知命题P：函数f（x）=
+lg（3-x）的定义域为（2，3），命题Q：已知
，
为非零向量，则“函数f（x）=（
x+
）2为偶函数”是“
⊥
”的充分但不必要条件．则下列命题为真命题的有（ ）
| 3x | ||
|
| a |
| b |
| a |
| b |
| a |
| b |
| A、P∧Q |
| B、P∧（￢Q） |
| C、（￢P）∧Q |
| D、（￢P）∨Q |
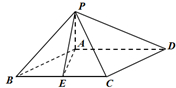如图，在四棱锥P-ABCD中，底面ABCD为菱形，∠ABC=60°，又PA⊥底面ABCD，AB=2PA，E为BC的中点．