Question

19．已知变量x，y满足$\left\{\begin{array}{l}{x-2y+4≥0}\\{x≤2}\\{x+y-2≥0}\end{array}\right.$，则$\frac{x+y+3}{x+2}$的取值范围是[$\frac{5}{4}$，$\frac{5}{2}$]．

Answer 1

分析 作出可行域，变形目标函数可得$\frac{x+y+3}{x+2}$=1+$\frac{y+1}{x+2}$表示可行域内的点与A（-2，-1）连线的斜率与1的和，数形结合可得．

解答 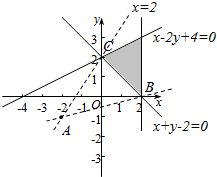解：作出$\left\{\begin{array}{l}{x-2y+4≥0}\\{x≤2}\\{x+y-2≥0}\end{array}\right.$所对应的区域（如图阴影），
变形目标函数可得$\frac{x+y+3}{x+2}$=$\frac{x+2+y+1}{x+2}$=1+$\frac{y+1}{x+2}$，
表示可行域内的点与A（-2，-1）连线的斜率与1的和，
由图象可知当直线经过点B（2，0）时，目标函数取最小值1+$\frac{0+1}{2+2}$=$\frac{5}{4}$；
当直线经过点C（0，2）时，目标函数取最大值1+$\frac{2+1}{0+2}$=$\frac{5}{2}$；
故答案为：[$\frac{5}{4}$，$\frac{5}{2}$]

点评 本题考查简单线性规划，涉及直线的斜率公式，准确作图是解决问题的关键，属中档题．