题目内容
2. 如图,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F 分别是 BC,PC的中点.
如图,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F 分别是 BC,PC的中点.(1)证明:AE⊥平面PAD
(2)取AB=2,若H为PD上的动点,EH与平面PAD所成最大角的正切值为$\frac{\sqrt{6}}{2}$时,求VP-AEH的体积.
分析 (1)由四边形ABCD为菱形,∠ABC=60°,推导出AE⊥BC,再由BC∥AD,得AE⊥AD,由PA⊥平面ABCD,得PA⊥AE,由此能证明AE⊥平面PAD.
(2)设AB=2,H为PD上任意一点,连结AH,EH,AE⊥平面PAD,则∠EHA为EH与平面PAD所成的角,当AH⊥PD时,∠EHA最大.此时tan∠EHA=$\frac{\sqrt{6}}{2}$,AH=$\sqrt{2}$,VP-AEH的体积VP-AEH=VE-PAH,由此能求出结果.
解答 证明:(1)由四边形ABCD为菱形,∠ABC=60°,可得△ABC为正三角形.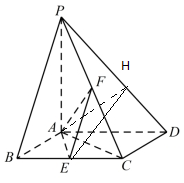
∵E为BC的中点,∴AE⊥BC.
又BC∥AD,因此AE⊥AD.
∵PA⊥平面ABCD,AE?平面ABCD,∴PA⊥AE.
而PA?平面PAD,AD?平面PAD且PA∩AD=A,
∴AE⊥平面PAD.
解:(2)设AB=2,H为PD上任意一点,连结AH,EH.
由(1)知AE⊥平面PAD,则∠EHA为EH与平面PAD所成的角.
在Rt△EAH中,AE=$\sqrt{3}$,
∴当AH最短时,∠EHA最大,
即当AH⊥PD时,∠EHA最大.此时tan∠EHA=$\frac{\sqrt{6}}{2}$,
因此AH=$\sqrt{2}$.
又AD=2,∴∠ADH=45°,∴PA=AD tan 45°=2.
∴VP-AEH=VE-PAH=$\frac{1}{3}{S}_{△PAH}•AE$
=$\frac{1}{3}(\frac{1}{2}×AH×PH)×AE$
=$\frac{1}{3}×(\frac{1}{2}×\sqrt{2}×\sqrt{2})×\sqrt{3}$
=$\frac{\sqrt{3}}{3}$.
点评 本题考查线面垂直的证明,考查三棱锥的体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

 阅读快车系列答案
阅读快车系列答案
| A. | 2n+1 | B. | 3n | C. | $\frac{{n}^{2}+2n}{2}$ | D. | $\frac{{n}^{2}+3n+2}{2}$ |
 一次考试中,五名学生的数学、物理成绩如下表所示:
一次考试中,五名学生的数学、物理成绩如下表所示:| 学生 | A | B | C | D | E |
| 数学成绩x(分) | 89 | 91 | 93 | 95 | 97 |
| 物理成绩y(分) | 87 | 89 | 89 | 92 | 93 |
(2)要从5名学生中选2人参加一项活动,求选中的学生中至少有一人的物理成绩高于90分的概率.
参考公式:回归直线的方程:$\widehaty=\widehatbx+\widehata$,其中$\widehatb=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.
| A. | y=±x | B. | y=±3x | C. | y=±$\sqrt{3}$x | D. | y=±$\frac{\sqrt{3}}{3}$x |
| A. | 1 | B. | 2 | C. | $\frac{3}{2}$ | D. | 3 |
 如图所示,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,A1、A2、B1、B2是椭圆的四个顶点,且$\overrightarrow{{A}_{1}{B}_{1}}$•$\overrightarrow{{A}_{2}{B}_{2}}$=3.
如图所示,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,A1、A2、B1、B2是椭圆的四个顶点,且$\overrightarrow{{A}_{1}{B}_{1}}$•$\overrightarrow{{A}_{2}{B}_{2}}$=3.