题目内容
一动圆与圆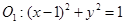 外切,与圆
外切,与圆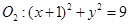 内切.
内切.
(1)求动圆圆心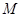 的轨迹
的轨迹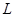 的方程;
的方程;
(2)设过圆心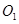 的直线
的直线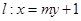 与轨迹
与轨迹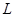 相交于
相交于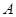 、
、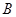 两点,请问
两点,请问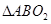 (
(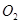 为圆
为圆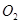 的圆心)的内切圆
的圆心)的内切圆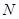 的面积是否存在最大值?若存在,求出这个最大值及直线
的面积是否存在最大值?若存在,求出这个最大值及直线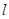 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
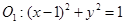 外切,与圆
外切,与圆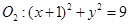 内切.
内切.(1)求动圆圆心
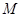 的轨迹
的轨迹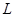 的方程;
的方程;(2)设过圆心
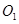 的直线
的直线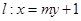 与轨迹
与轨迹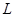 相交于
相交于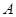 、
、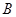 两点,请问
两点,请问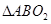 (
(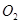 为圆
为圆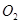 的圆心)的内切圆
的圆心)的内切圆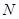 的面积是否存在最大值?若存在,求出这个最大值及直线
的面积是否存在最大值?若存在,求出这个最大值及直线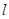 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.(1)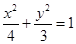 .
.
(2)存在直线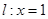 ,
,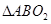 的内切圆M的面积最大值为
的内切圆M的面积最大值为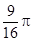
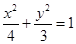 .
.(2)存在直线
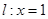 ,
,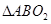 的内切圆M的面积最大值为
的内切圆M的面积最大值为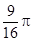
1)设动圆圆心为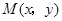 ,半径为
,半径为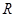 .
.
由题意,得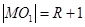 ,
,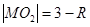 ,
,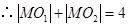 . …………3分
. …………3分
由椭圆定义知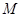 在以
在以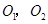 为焦点的椭圆上,且
为焦点的椭圆上,且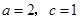 ,
,
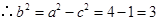 .
.
 动圆圆心M的轨迹
动圆圆心M的轨迹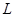 的方程为
的方程为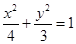 .……6分
.……6分
(2) 如图,设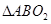 内切圆N的半径为
内切圆N的半径为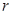 ,与直线
,与直线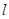 的切点为C,
的切点为C,
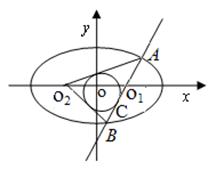
则三角形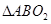 的面积
的面积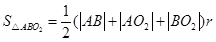
=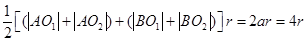
当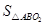 最大时,
最大时,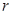 也最大,
也最大, 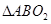 内切圆的面积也最大, …………7分
内切圆的面积也最大, …………7分
设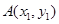 、
、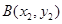 (
(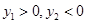 ),则
),则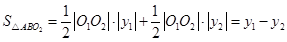 , ……8分
, ……8分
由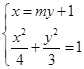 ,得
,得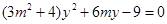 ,
,
解得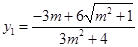 ,
,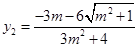 , …………10分
, …………10分
∴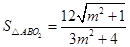 ,令
,令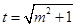 ,则
,则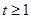 ,且
,且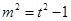 ,
,
有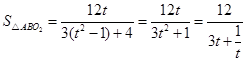 ,令
,令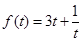 ,则
,则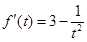 ,
,
当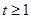 时,
时,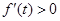 ,
,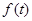 在
在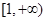 上单调递增,有
上单调递增,有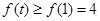 ,
,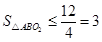 ,
,
即当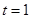 ,
,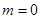 时,
时,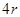 有最大值
有最大值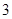 ,得
,得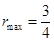 ,这时所求内切圆的面积为
,这时所求内切圆的面积为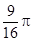 ,
,
∴存在直线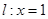 ,
,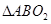 的内切圆M的面积最大值为
的内切圆M的面积最大值为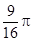 . …………14分
. …………14分
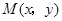 ,半径为
,半径为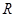 .
.由题意,得
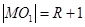 ,
,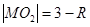 ,
,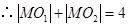 . …………3分
. …………3分由椭圆定义知
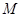 在以
在以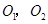 为焦点的椭圆上,且
为焦点的椭圆上,且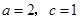 ,
,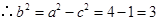 .
. 动圆圆心M的轨迹
动圆圆心M的轨迹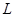 的方程为
的方程为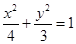 .……6分
.……6分(2) 如图,设
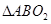 内切圆N的半径为
内切圆N的半径为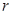 ,与直线
,与直线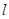 的切点为C,
的切点为C,
则三角形
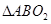 的面积
的面积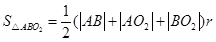
=
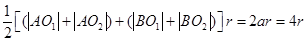
当
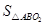 最大时,
最大时,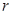 也最大,
也最大, 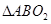 内切圆的面积也最大, …………7分
内切圆的面积也最大, …………7分设
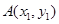 、
、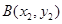 (
(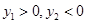 ),则
),则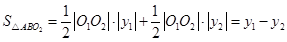 , ……8分
, ……8分由
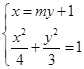 ,得
,得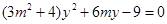 ,
,解得
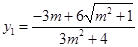 ,
,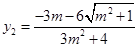 , …………10分
, …………10分∴
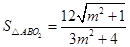 ,令
,令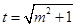 ,则
,则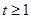 ,且
,且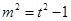 ,
,有
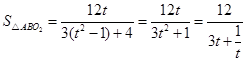 ,令
,令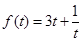 ,则
,则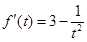 ,
,当
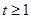 时,
时,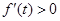 ,
,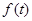 在
在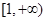 上单调递增,有
上单调递增,有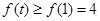 ,
,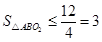 ,
,即当
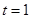 ,
,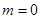 时,
时,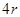 有最大值
有最大值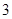 ,得
,得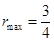 ,这时所求内切圆的面积为
,这时所求内切圆的面积为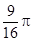 ,
,∴存在直线
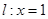 ,
,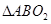 的内切圆M的面积最大值为
的内切圆M的面积最大值为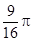 . …………14分
. …………14分
练习册系列答案
相关题目
 ,
,


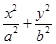 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为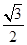 ,且在x轴上的顶点分别为
,且在x轴上的顶点分别为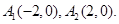
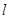 :
: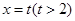 与
与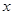 轴交于点T,P为
轴交于点T,P为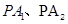 分别与椭圆交于M、N两点,试问直线MN是否通过椭圆的焦点?并证明你的结论.
分别与椭圆交于M、N两点,试问直线MN是否通过椭圆的焦点?并证明你的结论.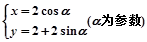 ,M是曲线C1上
,M是曲线C1上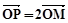
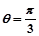 与曲线C1、C2交于不同于极点的A、B两点,求|AB|.
与曲线C1、C2交于不同于极点的A、B两点,求|AB|.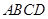 的两条对角线相交于点
的两条对角线相交于点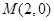 ,
,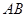 边所在直线的方程为
边所在直线的方程为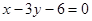 ,点
,点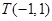 在
在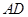 边所在直线上。
边所在直线上。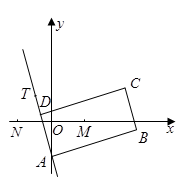
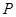 过点
过点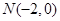 ,且与矩形
,且与矩形 上的点到直线
上的点到直线 的最近距离是
的最近距离是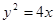 上一点
上一点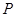 作圆
作圆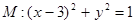 的两条切线,切点为
的两条切线,切点为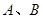 ,当四边形
,当四边形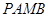 的面积最小时,直线
的面积最小时,直线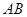 的方程为 .
的方程为 .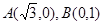 ,圆
,圆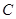 是以
是以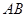 为直径的圆,直线
为直径的圆,直线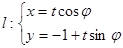 ,(
,(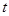 为参数).
为参数).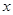 轴正半轴为极轴,建立极坐标系,求圆
轴正半轴为极轴,建立极坐标系,求圆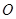 作直线
作直线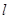 的垂线,垂足为
的垂线,垂足为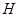 ,若动点
,若动点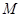 满足
满足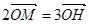 ,当
,当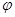 变化时,求点
变化时,求点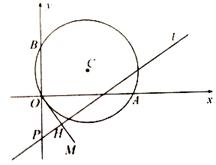
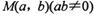 是圆
是圆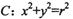 内一点,直线l是以M为中点的弦所在的直线,直线m的方程为
内一点,直线l是以M为中点的弦所在的直线,直线m的方程为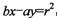 ,那么
,那么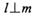 且m与圆C相切
且m与圆C相切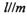 且/W与圆C相切
且/W与圆C相切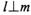 且m与圆C相离
且m与圆C相离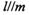 且w与圆C相离
且w与圆C相离