题目内容
【题目】已知椭圆
:
的左右顶点分别为
,
,
为坐标原点,且
.
(1)求椭圆的标准方程；
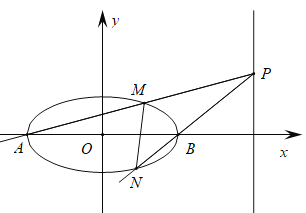
(2)若点
为直线
在第一象限内的一点,连接
交椭圆于点
,连接
并延长交椭圆于点
.若直线
的斜率为1,求点的坐标.
【答案】（1）
（2）
【解析】
（1）根据椭圆的几何意义,求得
进而求得
,即可得椭圆的标准方程.
（2）根据直线
的斜率为1,可设直线的方程,联立椭圆方程,利用直线与椭圆有两个交点可知
得
的范围.由两点求得斜率并表示出直线
与直线
,结合韦达定理即可求得的值.即可得
点的坐标.
（1）根据椭圆的几何意义,可知
，
所以
，故椭圆
:；
（2）因为直线的斜率为1，所以设:
,
,
，
与椭圆联立
，整理得
，
，
则
,
，
直线:
与直线:
交于点，
则
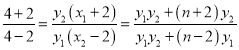
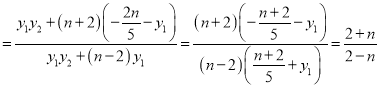，故
，
点在第一象限则
，由于点
，直线的方程为
，
联立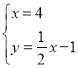
，解得
，故.
练习册系列答案
相关题目
【题目】科研人员在对人体脂肪含量和年龄之间关系的研究中，获得了一些年龄和脂肪含量的简单随机样本数据，如下表：
| 26 | 27 | 39 | 41 | 49 | 53 | 56 | 58 | 60 | 61 |
| 14.5 | 17.8 | 21.2 | 25.9 | 26.3 | 29.6 | 31.4 | 33.5 | 35.2 | 34.6 |
根据上表的数据得到如下的散点图.
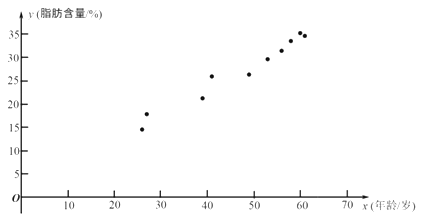
（1）根据上表中的样本数据及其散点图：
（i）求
；
（i）计算样本相关系数（精确到0.01），并刻画它们的相关程度.
（2）若
关于
的线性回归方程为
，求
的值（精确到0.01），并根据回归方程估计年龄为50岁时人体的脂肪含量.
附：参考数据：
，
，
，
，
，
，
参考公式：相关系数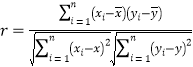
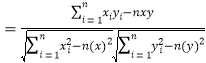
回归方程
中斜率和截距的最小二乘估计公式分别为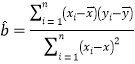
，
.
