题目内容
1.函数f(x)=$\frac{\sqrt{1-{x}^{2}}-1}{x-2}$的取值范围为[0,1].分析 令x=cosθ(0≤θ≤π)换元,化简后利用$y=\frac{sinθ-1}{cosθ-1}$(0≤θ≤π)的几何意义求得答案.
解答 解:由1-x2≥0,得-1≤x≤1,
令x=cosθ(0≤θ≤π),
则函数f(x)=$\frac{\sqrt{1-{x}^{2}}-1}{x-2}$化为y=$\frac{\sqrt{1-co{s}^{2}θ}-1}{cosθ-2}$=$\frac{\sqrt{si{n}^{2}θ}-1}{cosθ-2}=\frac{sinθ-1}{cosθ-2}$,
其几何意义为单位圆上半圆与定点P(2,1)连线的斜率,
如图: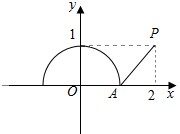
∵${k}_{AP}=\frac{1-0}{2-1}=1$,
∴函数f(x)=$\frac{\sqrt{1-{x}^{2}}-1}{x-2}$的取值范围为[0,1].
故答案为:[0,1].
点评 本题考查函数值域的求法,考查了换元法,体现了数形结合的解题思想方法,是中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
16.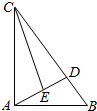 如图所示,在Rt△ABC中,∠BAC=90°,AB=2,BC=4,BD=$\frac{1}{4}$BC,E是AD的中点,则$\overrightarrow{CE}$$•\overrightarrow{AB}$的值是( )
如图所示,在Rt△ABC中,∠BAC=90°,AB=2,BC=4,BD=$\frac{1}{4}$BC,E是AD的中点,则$\overrightarrow{CE}$$•\overrightarrow{AB}$的值是( )
 如图所示,在Rt△ABC中,∠BAC=90°,AB=2,BC=4,BD=$\frac{1}{4}$BC,E是AD的中点,则$\overrightarrow{CE}$$•\overrightarrow{AB}$的值是( )
如图所示,在Rt△ABC中,∠BAC=90°,AB=2,BC=4,BD=$\frac{1}{4}$BC,E是AD的中点,则$\overrightarrow{CE}$$•\overrightarrow{AB}$的值是( )| A. | 3 | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | $\frac{3}{2}$ |
6.已知命题p:?m∈R,使得函数f(x)=x3+(m-1)x2-2是奇函数,命题q:向量$\overrightarrow{a}$=(x1,y1),$\overrightarrow{b}$=(x2,y2),则“$\frac{{x}_{1}}{{x}_{2}}$=$\frac{{y}_{1}}{{y}_{2}}$”是:“$\overrightarrow{a}$∥$\overrightarrow{b}$”的充要条件,则下列命题为真命题的是( )
| A. | p∧q | B. | (¬p)∧q | C. | p∧(¬q) | D. | (¬p)∧(¬q) |
11.函数f(x)=sin(x+$\frac{π}{3}$)+sin(x-$\frac{π}{3}$)的最大值是( )
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\sqrt{3}$ |