题目内容
13.已知F1,F2是双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点,直线y=a与双曲线两条渐近线的左、右交点分别为A,B,若四边形ABF2F1的面积为5ab,则双曲线的离心率为( )| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
分析 求出双曲线的渐近线,联立方程求出A,B的坐标,结合梯形的面积公式进行求解转化即可.
解答 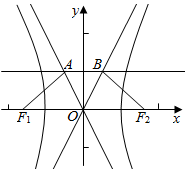 解:双曲线的渐近线方程为y=±$\frac{b}{a}$x,
解:双曲线的渐近线方程为y=±$\frac{b}{a}$x,
由±$\frac{b}{a}$x=a,得x=±$\frac{{a}^{2}}{b}$,即A(-$\frac{{a}^{2}}{b}$,a),B($\frac{{a}^{2}}{b}$,a)
则AB=$\frac{2{a}^{2}}{b}$,|F1F2|=2c,
则四边形ABF2F1的面积为S=$\frac{(\frac{2{a}^{2}}{b}+2c)×a}{2}$=($\frac{{a}^{2}}{b}$+c)a=5ab,
即$\frac{{a}^{2}}{b}$+c=5b,即a2+bc=5b2,
则c2-b2+bc=5b2,
即c2+bc-6b2=0,
则(c-2b)(c+3b)=0,
得c=2b或c=-3b(舍),
则c2=4b2=4c2-4a2,
即3c2=4a2,
即$\sqrt{3}$c=2a,
则$\frac{c}{a}$=$\frac{2}{\sqrt{3}}$=$\frac{{2\sqrt{3}}}{3}$,
即双曲线的离心率e=$\frac{{2\sqrt{3}}}{3}$,
故选:A
点评 本题主要考查双曲线离心率的计算,根据条件建立方程组关系求出交点坐标,结合梯形的面积公式进行转化是解决本题的关键.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
3.以下四个命题,属于组合问题的是( )
| A. | 从3个不同的小球中,取出2个排成一列 | |
| B. | 老师在排座位时将甲、乙两位同学安排为同桌 | |
| C. | 在电视节目中,主持人从100位幸运观众中选出2名幸运之星 | |
| D. | 从某班40名学生中选取5名学生,并从低到高依次排列 |
1.已知实数1,m,4构成一个等比数列,则圆锥曲线$\frac{{x}^{2}}{m}$+y2=1的离心率为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{2}}{2}$或$\sqrt{3}$ | D. | $\frac{\sqrt{2}}{2}$或$\frac{\sqrt{6}}{2}$ |
18.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的实轴的两个端点和虚轴的两个端点恰好构成一个正方形,则此双曲线的离心率为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
2.设集合M={x|(x-3)(x+2)<0},N={x|x-1>0},则M∩N=( )
| A. | (1,2) | B. | (1,3) | C. | (-1,2) | D. | (-1,3) |
