题目内容
解不等式：x2-mx-1-m＞0．
考点：一元二次不等式的解法
专题：不等式的解法及应用
分析：原不等式可化为（x+1）（x-1-m）＞0，分m=-2和m＜-2以及m＞-2可得解集．
解答：
解：原不等式可化为（x+1）（x-1-m）＞0，
当-1-m=1即m=-2时，原不等式可化为（x+1）2＞0，解集为{x|x≠-1}；
当-1-m＞1即m＜-2时，原不等式的解集为{x|x＜1或x＞-1-m}；
当-1-m＜1即m＞-2时，原不等式的解集为{x|x＜-1-m或x＞1}
当-1-m=1即m=-2时，原不等式可化为（x+1）2＞0，解集为{x|x≠-1}；
当-1-m＞1即m＜-2时，原不等式的解集为{x|x＜1或x＞-1-m}；
当-1-m＜1即m＞-2时，原不等式的解集为{x|x＜-1-m或x＞1}
点评：本题考查含参数的不等式的解集，涉及分类讨论的思想，属基础题．
练习册系列答案
每课必练系列答案
相关题目
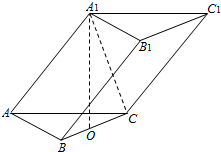在三棱柱ABC-A1B1C1中，已知AB=AC=AA1=