题目内容
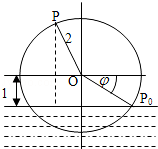
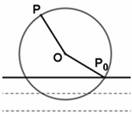
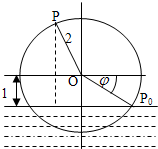 一半径为2m的水轮如图所示,水轮圆心O距离水面1m;已知水轮按逆时针做匀速转动,每3s转一圈,如果当水轮上点P从水中浮现时(图中点P0)开始计算时间.
一半径为2m的水轮如图所示,水轮圆心O距离水面1m;已知水轮按逆时针做匀速转动,每3s转一圈,如果当水轮上点P从水中浮现时(图中点P0)开始计算时间.
(1)试建立适当的坐标系,将点P距离水面的高度h(m)表示为时间t(s)的函数;
(2)点P第一次到达最高点大约要多长时间?
(3)记f(t)=h,求证:不论t为何值,f (t)+f (t+1)+f (t+2)是定值.
 解:(1)以水轮所在平面与水面的交线为x轴,以过点O且与水面垂直的直线为y轴,
解:(1)以水轮所在平面与水面的交线为x轴,以过点O且与水面垂直的直线为y轴,建立如图所示的直角坐标系,设h=Asin(ωt+?)+k,(-
 <?<0),
<?<0),则A=2,k=1,
∵T=3=
 ,
,∴ω=

∴h=2sin(
 t+?)+1,
t+?)+1,∵t=0,h=0,
∴0=2sin?+1,
∴sin?=-
 ,
,∵-
 <?<0,
<?<0,∴?=-
 ,
,∴h=2sin(
 t-
t- )+1
)+1(2)令2sin(
 t-
t- )+1=3,得sin(
)+1=3,得sin( t-
t- )=1,
)=1,∴
 t-
t- =
= ,
,∴t=1,
∴点P第一次到达最高点大约要1s的时间;
(3)由(1)知:f (t)=2sin(
 t-
t- )+1=
)+1= sin
sin t-cos
t-cos t+1,
t+1,f (t+1)=2sin(
 t+
t+ )+1=2cos
)+1=2cos t+1,
t+1,f (t+2)=2sin(
 t+
t+ )+1=-
)+1=- sin
sin t-cos
t-cos t+1,
t+1,∴f (t)+f (t+1)+f (t+2)=3(为定值).
分析:(1)先根据h的最大和最小值求得A和k,利用周期求得ω,当t=0时,h=0,进而求得φ的值,则函数的表达式可得;
(2)令最大值为3,可得三角函数方程,进而可求点P第一次到达最高点的时间;
(3)由(1)可求:f (t),f (t+1),f (t+2),进而可求f (t)+f (t+1)+f (t+2)是定值.
点评:本题以实际问题为载体,考查三角函数模型的构建,考查学生分析解决问题的能力,解题的关键是构建三角函数式,利用待定系数法求得.

练习册系列答案
相关题目
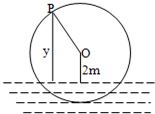 如图为一半径为3m的水轮,水轮中心O距水面2m,已知水轮每分钟旋转4圈,水轮上的点P到水面距离y(m)与时间x(t)满足函数关系y=Asin(ωx+φ)+2则( )
如图为一半径为3m的水轮,水轮中心O距水面2m,已知水轮每分钟旋转4圈,水轮上的点P到水面距离y(m)与时间x(t)满足函数关系y=Asin(ωx+φ)+2则( )A、ω=
| ||
B、ω=
| ||
C、ω=
| ||
D、ω=
|
 一半径为2m的水轮如图所示,水轮圆心O距离水面1m;已知水轮按逆时针做匀速转动,每3s转一圈,如果当水轮上点P从水中浮现时(图中点P0)开始计算时间.
一半径为2m的水轮如图所示,水轮圆心O距离水面1m;已知水轮按逆时针做匀速转动,每3s转一圈,如果当水轮上点P从水中浮现时(图中点P0)开始计算时间.