Question

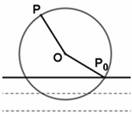
一半径为4m的水轮如图,水轮圆心O距离水面2m,已知水轮每分钟转动4圈,如果当水轮上点P从水中浮现时(图中点P₀)开始计时.

⑴将点P距离水面的高度z(m)表示为时间t(s)的函数.

⑵点P第一次到达最高点要多长时间？

 　⑶在水轮转动的一圈内，有多长时间点P距水面的高度不超过.

Answer 1

解：（1）建立如图所示的平面直角坐标系．

设角是以为始边，为终边的角．

易知在内所转过的角为，

故角是以为始边，为终边的角，

故点的纵坐标为，

则，

又当时，，，

，，

故所求函数关系式为；

（2）令，

则，即．

取，

解得，

故点第一次到达最高点大约需要．

（3）令

　　　　

　　　　

　　　　

　　　　∴在水轮转动的一圈内，有2.5s的时间点P距水面的高度不超过。